【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.5】ニューラルネットワークの実装(入力層・Affine前半)
1. 本記事について
本記事は、これまでの内容（ニューラルネットワークの理解その1〜4）を踏まえ、ニューラルネットワークをpythonプログラムに落とし込んでいきます。
本記事で入力層・中間層の実装を解説していきます。
ニューラルネットワークの理解その1~4を見てから、本記事を見ることをお勧めします（特にその4）。
注意事項として、本シリーズではpythonの基礎的な解説、numpyの基礎的な解説は割愛させていただきます。特に、numpy配列やshape等頻出なので、その辺の知識が不十分の場合は、そちらの習得を先に行うことをお勧めします。
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. pythonでの実装について
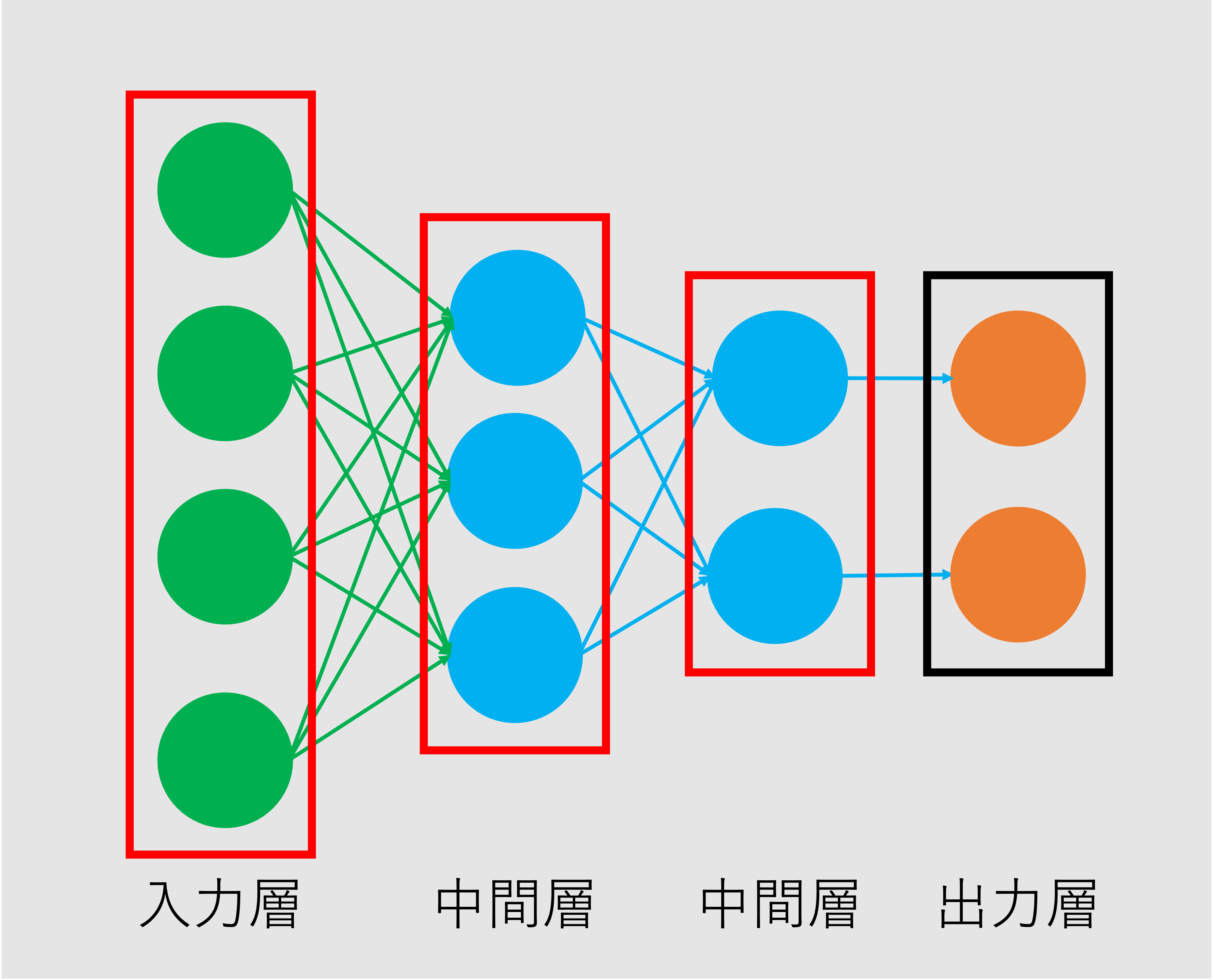図1 ニューラルネットワーク
今回は、図1の入力層、中間層をそれぞれpythonで実装していきたいと思います。
尚、図1の中間層には、実は名前があり、Affine層や全結合層と呼ばれます。ここではAffine層と呼ぶことにします。
3. 入力層
入力層は、正直特別な処理を全く行いません。ただnumpy配列を作成するのみです。
ここでは、xを入力とします。このxがニューラルネットワークの入力値として入力されます。
import numpy as np
# 入力: ノード数4
x = np.array([[0.24, 0.71, 0.19, 0.33]])
例として、4つのノードからなる入力層を想定しました。
xはそのまま次のAffine層へ渡されます。
4. Affine層
Affine層の処理をpythonで実装していきます。大きく順伝播の処理と逆伝播の処理に分けて実装します。
順伝播
順伝播（入力→出力へ向かう）の計算について見ていきます。
普通に入力から出力へ向かう計算ですので、重み付き線形和を実装していきます。計算についての詳細は、こちらを参照いただければと思います。
入力をx、重みをW、バイアスをbとします。
コードは以下になります。
import numpy as np
out = np.dot(x, W) + b
1行で終わりです。簡単ですね。
注意点として、xの列数とWの行数が一致している、また、Wの列数とbの要素数が一致している必要があります。
具体例として、xとWとbをそれぞれ以下とし、重み付き線形和outを算出してみます。
import numpy as np
# 入力: ノード数4
x = np.array([[0.24, 0.71, 0.19, 0.33]])
# 重み: 入力4 * 出力3
W = np.array([
[0.37, 0.52, 0.79],
[0.29, 0.83, 0.12],
[0.54, 0.77, 0.63],
[0.48, 0.29, 0.85]
])
# バイアス: ノード数3
b = np.array([[0.26, 0.42, 0.88]])
# 順伝播の計算
out = np.dot(x, W) + b
print(out)
print(out.shape)
[[0.8157 1.3761 1.555 ]]
(1, 3)
今回は、入力xが1行4列で、重みW4行3列、バイアスbが1行3列となっています。
上述した様に、入力のノード数と出力のノード数を確認して、Wやbの行列を決定します。
outが重み付き線形和として出力されます。outはその後活性化関数やロス関数へ渡されることになります。
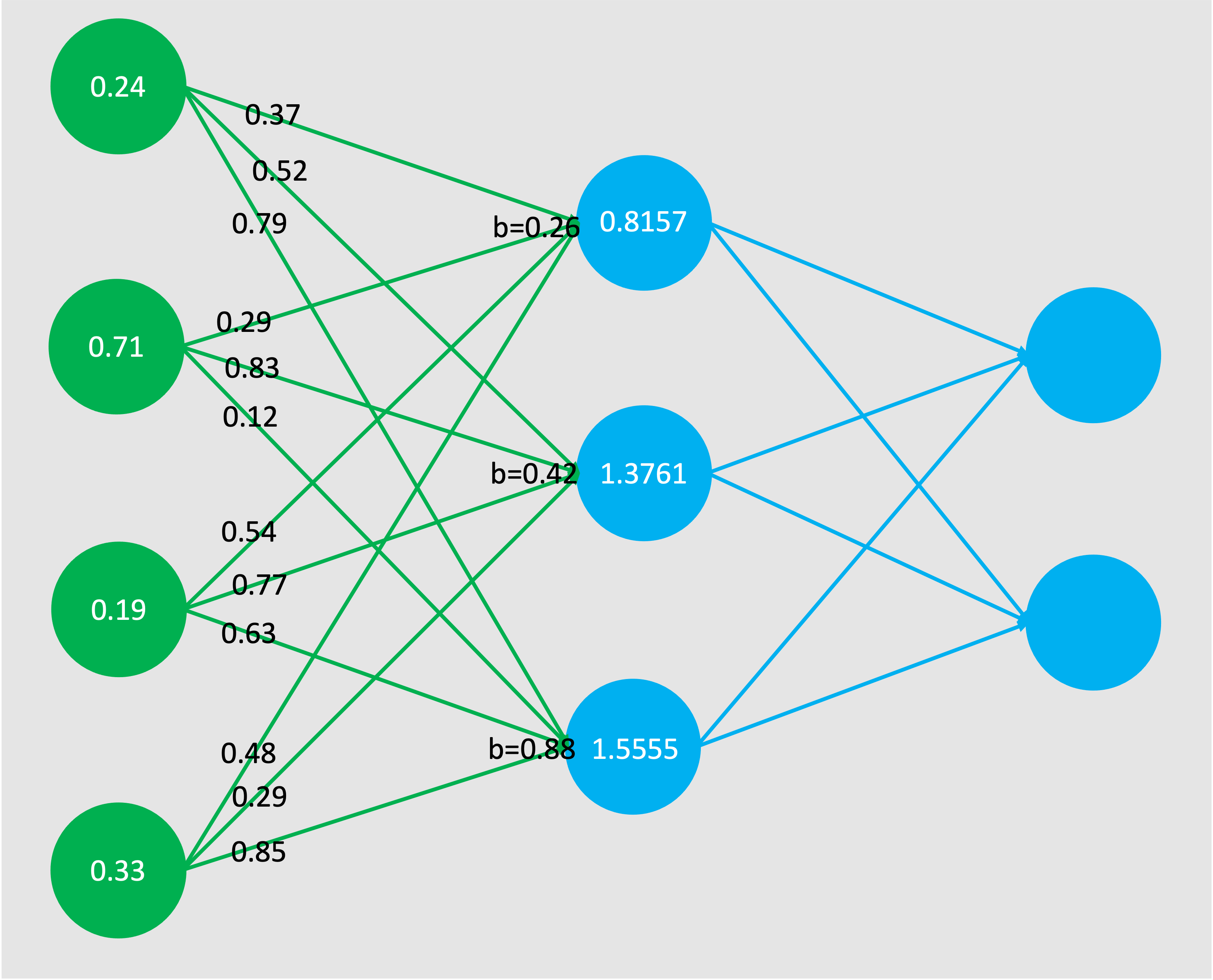図2 ニューラルネットワーク（図1に計算結果を当てはめたもの）
逆伝播
逆伝播（出力→入力へ向かう）の計算について見ていきます。
重み
まず、前回行った、誤差逆伝播法での\(Δw\)の計算式を以下に示します。
式1
\(Δw^L_{ij}\)の式が、出力層の\(Δw\)の計算です。
\(Δw^l_{ij}\)の式が、出力層以外の\(Δw\)の計算です
（計算についての詳細は、こちらを参照いただければと思います）。
尚、ここ（逆伝播のpython実装）では、実際に\(W\)の更新までの処理は行わないため、\(\frac{∂E}{∂w^l}\)を実装していきます。
式1を、pythonに落とし込んでいきます。
まず、pythonで実装する場合、出力層と出力層以外とで分けることはせず、統一の処理を実装します。
さらに、pythonでは\(l\)層にかかるノードをまとめて処理することができます。なので添字\(i\)や\(j\)、\(ij\)を考えなくてよくなります。
上記を踏まえ、式1を以下の様に1つの式で表します。
式2
\(\frac{∂E}{∂w^l}\)を\(δ^l\)と\(z^{l-1}\)の掛け算で表します。
式1において、
出力層の計算については、
右辺\((y_j - t_j)\)を\(δ^l\)としています。
出力層以外の計算については、
右辺\(\sum_k δ^{l+1}_k \times w^{l+1}_{jk} \times \frac{∂f^l(u^l_j)}{∂u^l_j}\)を\(δ^l\)としています。
この\(\frac{∂E}{∂w^l} = δ^l \times z^{l-1}\)について、
\(δ^l\)をdoutとします。
\(z^{l-1}\)をxとします。
\(\frac{∂E}{∂w^l}\)をdWとします。
※ \(z^{l-1}\)についてですが、これは「\(l-1\)層目の出力値」ということになります。
ということは、\(l\)層目、つまり今実装しようとしている層からすると入力値になります。
なので、\(z^{l-1}\)を、先ほど入力値として使用したxで表しています。
上記の条件で実装します。
import numpy as np
dW = np.dot(x.T, dout)
xを転置しています。x.Tとdoutを掛けることでdWがWと同じ行列数となります。
具体例として、xとdoutをそれぞれ以下とし、dWを算出してみます。
import numpy as np
# 入力: ノード数4
x = np.array([[0.24, 0.71, 0.19, 0.33]])
# δ: ノード数３
dout = np.array([[0.71, 0.57, 0.35]])
dW = np.dot(x.T, dout)
print(dW)
print(dW.shape)
[[0.1704 0.1368 0.084 ]
[0.5041 0.4047 0.2485]
[0.1349 0.1083 0.0665]
[0.2343 0.1881 0.1155]]
(4, 3)
これでdW、つまり\(\frac{∂E}{∂w^l}\)を実装できました。
ただし、実は逆伝播の計算はこれだけではありません。dWの他に、バイアスの更新量（\(Δb\)）と\(l-1\)層に渡す\(δ\)をそれぞれ実装する必要があります。
長くなってしまったので、これらの実装は次回解説させていただきます。
5. まとめ
今回はニューラルネットワークの実装（入力層・Affine層の途中まで）について解説しました。
次回も是非みてみてください！
6. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search