【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.1】ニューラルネットワークの理解(その1)

1. 本記事について

本シリーズの実質第1回目として、ニューラルネットワークがどういったものかについて解説していきます。その1〜その4の4回を予定しています。
理解が終わったら、実際にニューラルネットワークをPythonで実装していくという予定です。

ニューラルネットワークは、物体検出に限らず、ディープラーニングにおいて土台となる概念となりますので、まずはここの理解を進めていきます。

なお、本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。

非常に有名な書籍ですので、皆さんご存知かもしれませんが、もしご覧になったことがないという方は、めちゃくちゃおすすめです。

2016年初版で、だいぶ前の書籍ではありますが、深層学習の根本から解説されており、今読み返しても新たな発見があったりしますので、是非。

脱線してしまいましたが、上記書籍を参考にさせていただいております。

2. ニューラルネットワークについて

ニューラルネットワークとは、人間の脳内における処理を模して構築した学習モデルです。

図1　ニューラルネットワーク

図1を見ると、多数の丸と矢印が存在します。丸をニューロン（神経細胞）やノードといったりします。

図1の一番左側の層（\(x_1\)〜\(x_5\)）を入力層といいます。物体検出の場合、入力は画像データですので、入力層の1つ1つのノードには、各画素値が入力されます。
例えば、縦224ピクセル、横224ピクセルのカラー画像の場合、224*224*3=150528個のノードが存在することになります。
入力層は、後述する計算をした後、一つ右側の層へ数値を渡します。

図1の真ん中の層（\(z_1\)〜\(z_3\)）は中間層、若しくは隠れ層と呼ばれます。入力層から数値（物体検出の場合画素値）を受け取り、後述する計算をした後、次の中間層、若しくは出力層へ情報を渡します。
図1の場合、中間層は1層のみですが、基本的には何層も中間層が存在することがほとんどです。中間層が多ければ、その分より複雑な推論を行うことができるイメージです。

図1の一番右側の層（\(y_1\)、\(y_2\)）を出力層といいます。中間層から数値を受け取り、後述する計算をした後、最終的に数値を出力します。
例えば、YOLOv1の場合、1470個の出力ノードがあります（クラス=20）。 別の例として、画像認識で「犬」か「猫」を判別する場合、出力層は2つのノードになります。

この様に、入力層〜出力層まで、そのモデルによって、ノードの数や中間層の数は実に様々です。

3. ニューラルネットワークの計算

先ほど「後述する」と申し上げた、具体的な計算について解説します。

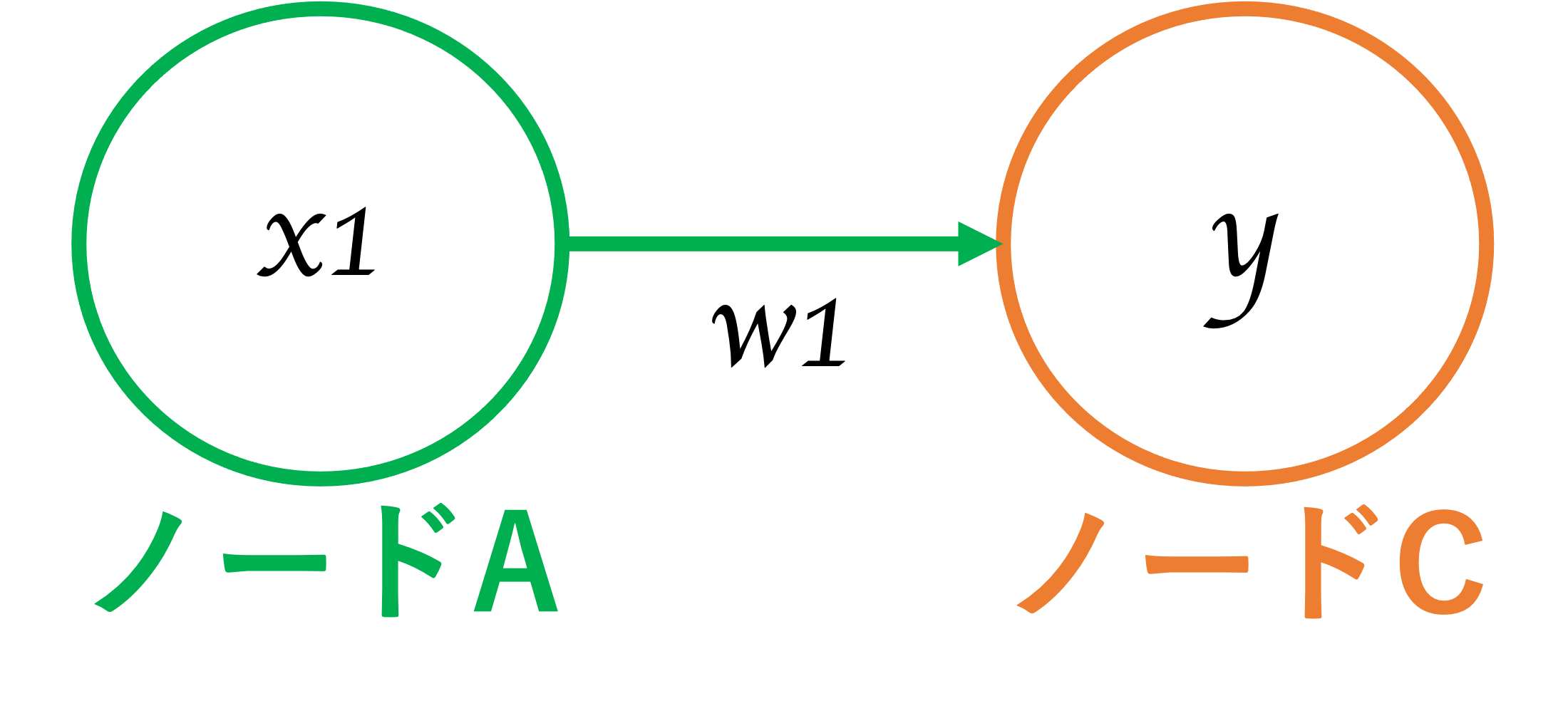図2　ニューラルネットワーク2

図2は、図1を簡略化したものになります。Cのノードを中心に見てみます。
CはAのノードから\(x_1\)という信号を受け取るのですが、その際\(x_1\)と\(w_1\)を乗算して受け取ります。\(w_1\)を重みといいます。
重みはそれぞれの信号に固有の数値です。

この時、ノードCが受け取る数値は以下となります。

式1

\( x_1 \times w_1 \)

ノードは、それぞれに閾値を持っており、渡された入力値が閾値を超えた場合、1を出力します。超えなければ0を出力します。
この時、\(y\)をノードCが出力する信号、\(θ\)をノードCが持っている閾値とします。\(y\)の式にすると以下になります。

式2

\( y = \left\{ \begin{eqnarray} 0 \quad (x_1 \times w_1 \leq θ) \\ 1 \quad (x_1 \times w_1 \gt θ) \end{eqnarray} \right. \)

単純にいうと、あるノードにおいて、入力信号が閾値を超えた場合次のノードへ信号を出力するという構造です。この構造は、脳の神経回路を参考に構成されています。

今後の処理の為に、式2を変形して以下にします。
尚、以下の\(b\)を「バイアス」と呼びます。

式3

\( y = \left\{ \begin{eqnarray} 0 \quad (x_1 \times w_1 + b \leq 0) \\ 1 \quad (x_1 \times w_1 + b \gt 0) \end{eqnarray} \right. \)

次に、入力のノードを1つ追加したモデルを例にみてみます。

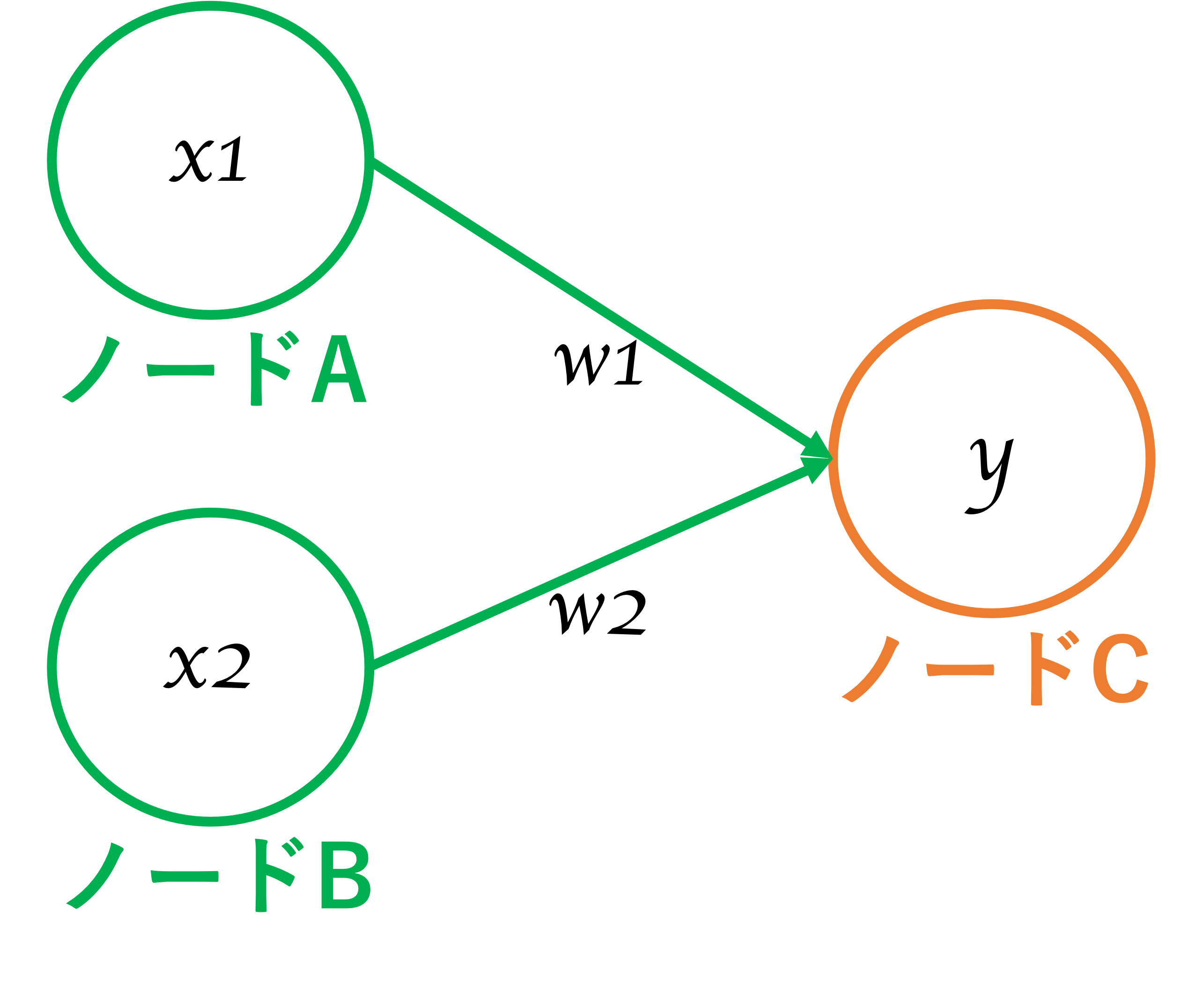図3　ニューラルネットワーク3

図3は、入力がAとBの2つのノードから受け取りますが、考え方は先ほどと同様です。
重みを乗算したそれぞれの入力値について総和をとります。

この時、ノードCが受け取る数値は以下となります。

式4

\( x_1 \times w_1 + x_2 \times w_2 \)

この時\(y\)の式は以下となります。

式5

\( y = \left\{ \begin{eqnarray} 0 \quad (x_1w_1 + x_2w_2 \leq θ) \\ 1 \quad (x_1w_1 + x_2w_2 \gt θ) \end{eqnarray} \right. \)

変形して以下となります。

式6

\( y = \left\{ \begin{eqnarray} 0 \quad (x_1w_1 + x_2w_2 + b \leq 0) \\ 1 \quad (x_1w_1 + x_2w_2 + b \gt 0) \end{eqnarray} \right. \)

4. 活性化関数について

式6に関して、以下の様に変形をします。

式7

\( y = f(x_1w_1 + x_2w_2 + b) \)

式7は、\(y=f(x)\)の形にしたものです。\(f(x)\)は、先程の「0を超えたら1になり、そうでなければ0になる」関数ということになります。
\(x\)には、ここでは \(x_1w_1 + x_2w_2 + b\) が代入されます。

この場合の\(f(x)\)関数には実は名前があり、ステップ関数という関数です。

式8

\( f(x) = \left\{ \begin{eqnarray} 0 \quad (x \lt 0) \\ 1 \quad (x \geq 0) \end{eqnarray} \right. \)

グラフにすると、以下の様になります。

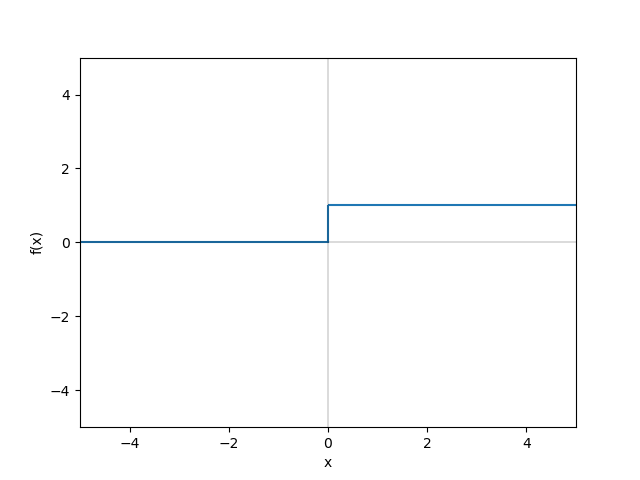グラフ　ステップ関数

今回のステップ関数のような、入力の総和をどの様に出力に繋げるか、その部分を司る関数を活性化関数といいます。

活性化関数にはいくつか種類があるのですが、本シリーズではYOLOv1に用いられているLeaky ReLUという活性化関数を解説します。

Leaky ReLUは、ReLUという活性化関数の派生系です。まずReLUがどういうものか解説します。

ReLU

ReLUは以下の式で表せます。

式9

\( f(x) = \left\{ \begin{eqnarray} 0 \quad (x \leq 0) \\ x \quad (x \gt 0) \end{eqnarray} \right. \)

入力値が0以下の時、出力値が常に0なります。入力値が0超の時、出力値が入力値と同じ値になります。
言葉ではわかりづらいと思いますので、グラフで確認してみます。

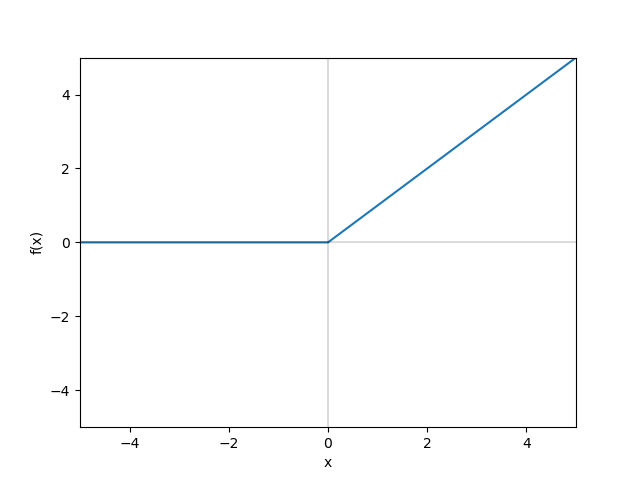グラフ　ReLU関数

Leaky ReLU

Leaky ReLUは以下の式で表せます。

式10

\( f(x) = \left\{ \begin{eqnarray} αx \quad (x \leq 0) \\ x \quad (x \gt 0) \end{eqnarray} \right. \)

ReLUは入力値が0以下の時、出力値が常に0でしたが、Leaky ReLUは0より下の値をとります。
こちらもグラフで確認した方がわかりやすいと思いますので、見てみます。

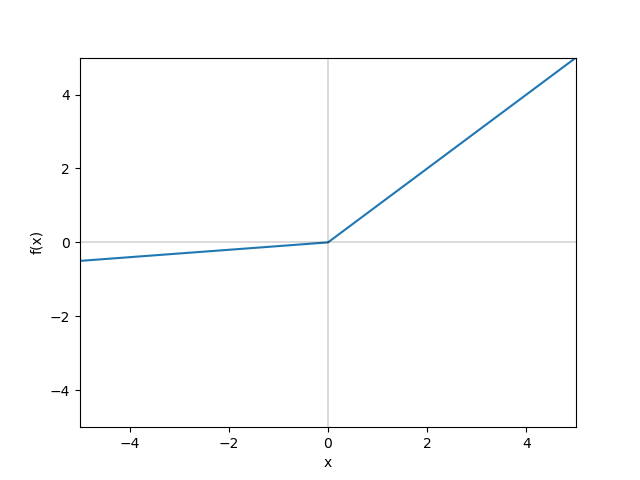グラフ　Leaky ReLU関数(\(α=0.1\))

Leakyの意味は「漏れている」だそうで、ReLUと比較して0以下の時に文字通り負の方向に「漏れている」形になります。

YOLOv1では、活性化関数にLeaky ReLUを採用しています。ですので、本シリーズでも、活性化関数は基本的にLeaky ReLUを使用します。

なお、式9の\(α\)は定数で、値は0.01をとることが多い様ですが、今回は\(α=0.1\)でいこうと思います。

5. 各層の入力処理

先述の内容をふまえ、各層毎の入力処理をみていこうと思います。

入力層→中間層

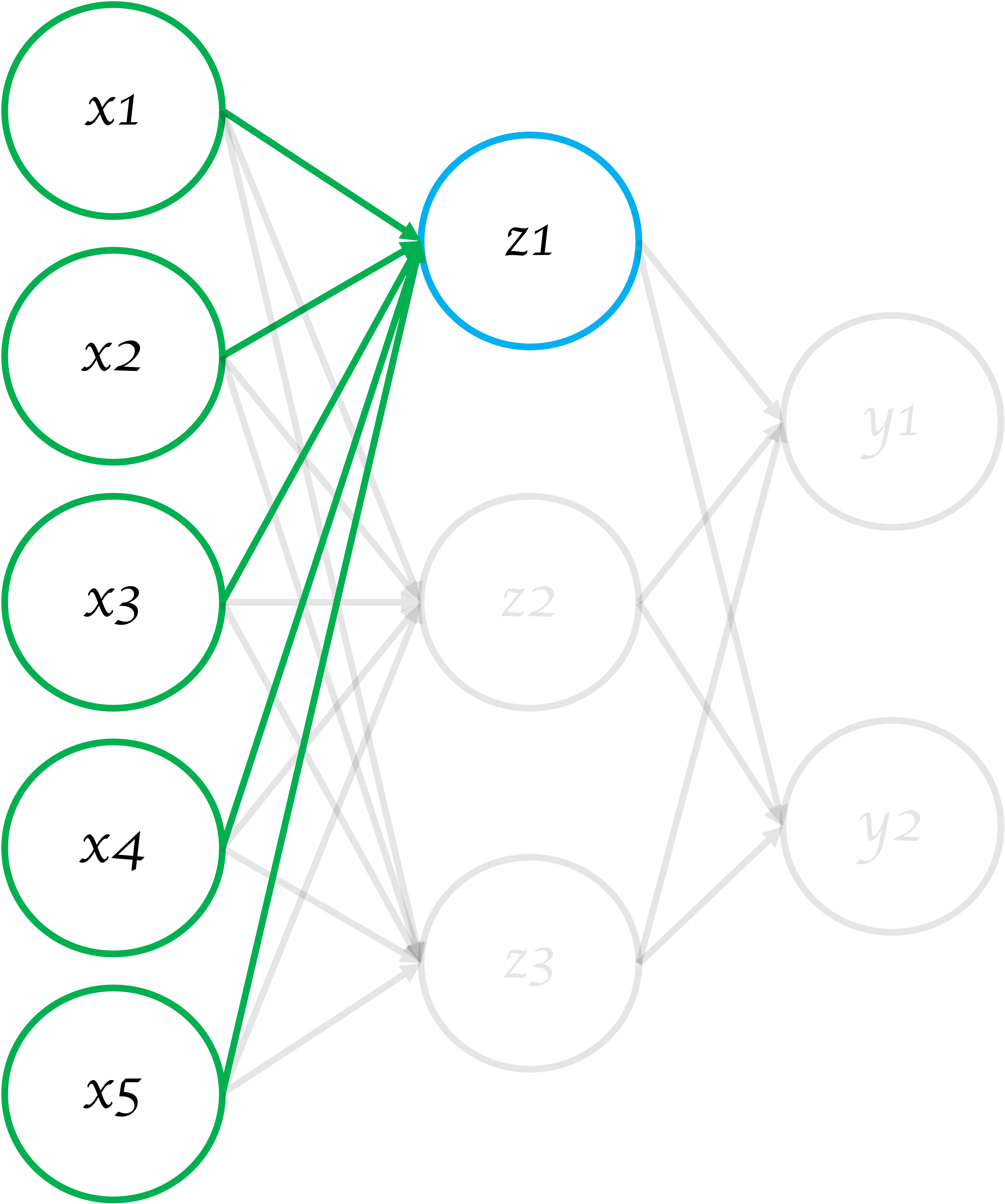図4　ニューラルネットワークの一部を抜粋1

図4で示した箇所について、式に表すと以下の様になります。

式11

\( a_1 = x_1w^{(1)}_{11} + x_2w^{(1)}_{21} + x_3w^{(1)}_{31} + x_4w^{(1)}_{41} + x_5w^{(1)}_{51} + b^{(1)}_1 \)
\( z_1 = f(a_1) \)

\(z_2\)、\(z_3\)についても同様に式に表します。

式12

\( a_2 = x_1w^{(1)}_{12} + x_2w^{(1)}_{22} + x_3w^{(1)}_{32} + x_4w^{(1)}_{42} + x_5w^{(1)}_{52} + b^{(1)}_2 \)
\( z_2 = f(a_2) \)

式13

\( a_3 = x_1w^{(1)}_{13} + x_2w^{(1)}_{23} + x_3w^{(1)}_{33} + x_4w^{(1)}_{43} + x_5w^{(1)}_{53} + b^{(1)}_3 \)
\( z_3 = f(a_3) \)

中間層→出力層

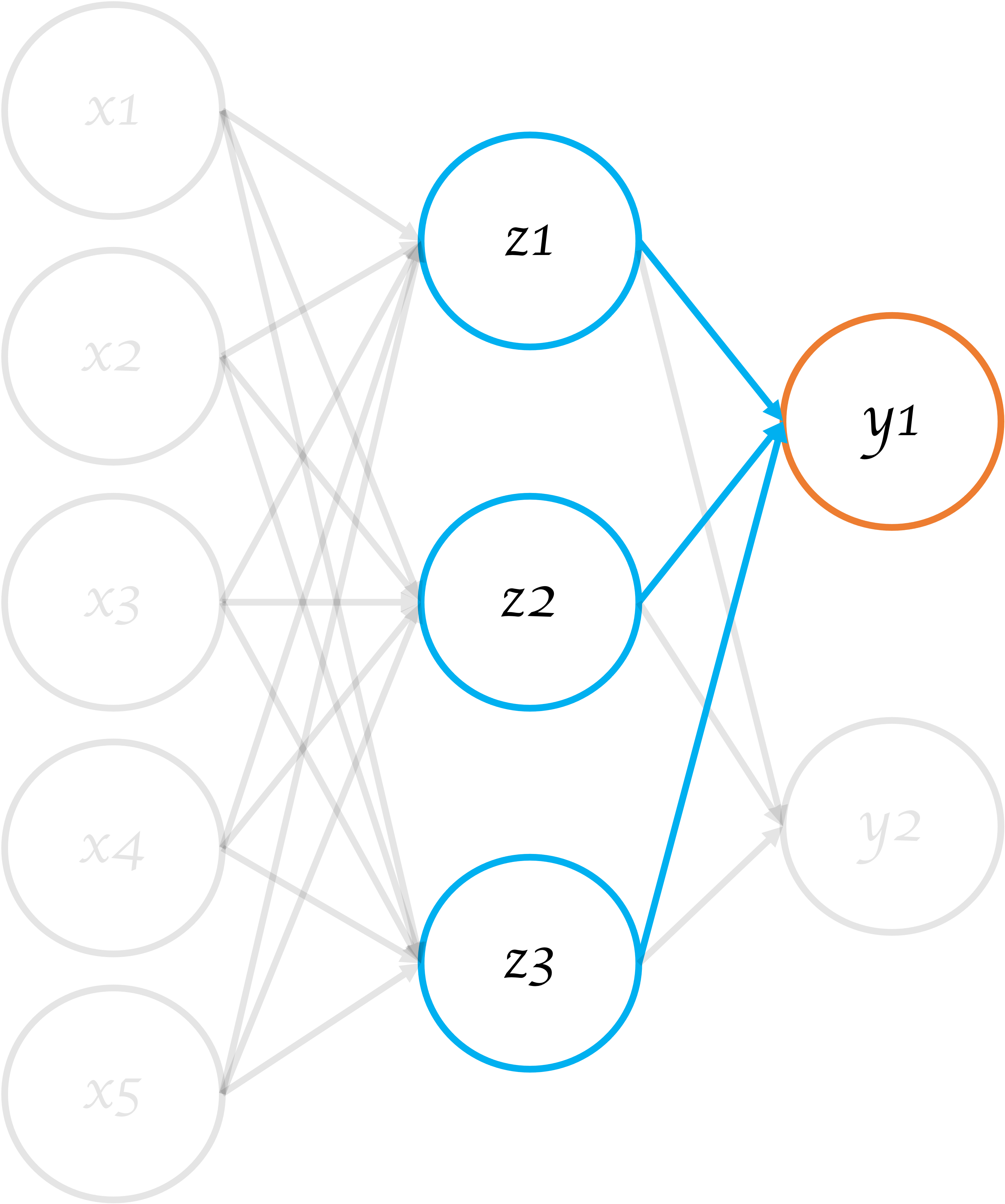図5　ニューラルネットワークの一部を抜粋2

中間層から出力層にかけての計算となります。
内容は入力層→出力層と同様ですが、活性化関数をする必要がないので（次へ伝達しない為）、当該計算は行いません。

式14

\( y_1 = z_1w^{(2)}_{11} + z_2w^{(2)}_{21} + z_3w^{(2)}_{31} + b^{(2)}_1 \)

式15

\( y_2 = z_1w^{(2)}_{12} + z_2w^{(2)}_{22} + z_3w^{(2)}_{32} + b^{(2)}_2 \)

以上で全ての式が出揃いましたので、最後に、具体的に入力から出力までの計算を行ってみます。

入力値と重みを以下の様にします(各値は適当です)。

式16

\( x_1 = 2 \) \( x_2 = 5 \) \( x_3 = 3 \) \( x_4 = 7 \) \( x_5 = 1 \) \( \) \( w^{(1)}_{11} = 0.43 \) \( w^{(1)}_{21} = 0.33 \) \( w^{(1)}_{31} = 0.9 \) \( w^{(1)}_{41} = 0.44 \) \( w^{(1)}_{51} = 0.04 \) \( \) \( w^{(1)}_{12} = 0.58 \) \( w^{(1)}_{22} = 0.57 \) \( w^{(1)}_{32} = 0.06 \) \( w^{(1)}_{42} = 0.41 \) \( w^{(1)}_{52} = 0.63 \) \( \) \( w^{(1)}_{13} = 0.22 \) \( w^{(1)}_{23} = 0.96 \) \( w^{(1)}_{33} = 0.06 \) \( w^{(1)}_{43} = 0.13 \) \( w^{(1)}_{53} = 0.85 \) \( \) \( w^{(2)}_{11} = 0.65 \) \( w^{(2)}_{21} = 0.45 \) \( w^{(2)}_{31} = 0.81 \) \( \) \( w^{(2)}_{12} = 0.75 \) \( w^{(2)}_{22} = 0.31 \) \( w^{(2)}_{32} = 0.01 \) \( \) \( b^{(1)}_1 = 0.03 \) \( b^{(1)}_2 = 0.42 \) \( b^{(1)}_3 = 0.76 \) \( b^{(2)}_1 = 0.58 \) \( b^{(2)}_2 = 0.29 \) \( \)

式16を元に、ニューラルネットワークの式11〜式15を計算します。

式17

\( \begin{eqnarray} a_1 = 2 \times 0.43 + 5 \times 0.33 + 3 \times 0.9 \\ + 7 \times 0.44 + 1 \times 0.04 + 0.03 = 8.36 \end{eqnarray} \)
\( z_1 = 8.36 \)
\( \begin{eqnarray} a_2 = 2 \times 0.58 + 5 \times 0.57 + 3 \times 0.06 \\ + 7 \times 0.41 + 1 \times 0.63 + 0.42 = 8.11 \end{eqnarray} \)
\( z_2 = 8.11 \)
\( \begin{eqnarray} a_3 = 2 \times 0.22 + 5 \times 0.96 + 3 \times 0.06 \\ + 7 \times 0.13 + 1 \times 0.85 + 0.76 = 7.94 \end{eqnarray} \)
\( z_3 = 7.94 \)
\( \begin{eqnarray} y_1 = 8.36 \times 0.65 + 8.11 \times 0.45 \\ + 7.94 \times 0.81 + 0.58 = 16.0949 \end{eqnarray} \)
\( \begin{eqnarray} y_2 = 8.36 \times 0.75 + 8.11 \times 0.31 \\ + 7.94 \times 0.01 + 0.29 = 9.1535 \end{eqnarray} \)

最終的に、最終的な出力値(\(y1\)、\(y2\))は以下の様になりました。

\( y_1 = 16.0949 \) \( y_2 = 9.1535 \)

ニューラルネットワークにおける、入力から出力への基本的な処理は以上になります。

物体検出のモデルにおいて、ニューラルネットワークでの処理を経た出力値\(y\)は、この後ロス関数へ渡されていくことになります。

6. まとめ

今回はニューラルネットワークについての概要と実際の計算について解説しました。
また、活性化関数について解説しました。

次回も是非みてみてください！

7. 参考文献

斎藤康毅　著　「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」

・物体検出AIの導入
・アノテーションサービス
・手書き計算サイト ZONE++ の運営
・技術ブログ LAB++の運営
   上記をメインにおこなっております

詳しくはこちら

Category

Link

Search

Archives