【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.4】ニューラルネットワークの理解(その4)

1. 本記事について

本記事はニューラルネットワークがどういったものかについて解説していきます。その1〜その4の4回を予定しており、本記事はその4です。

本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。

本記事は、上記書籍を参考にさせていただいております。

2. 誤差逆伝播法とは

誤差逆伝播法とは、あえて一言でいうと「ニューラルネットワークにおける、微分の計算方法」となります。

詳しい内容は後述しますが、よく前回解説した勾配法と混同されがちです。
以下の様な理解をするとすっきりいくと思います。

パラメータ（重みとバイアス）を最適化する為に、勾配法を使用している。

勾配法は以下の式で計算する。

\( W = W - ΔW \) \( ΔW = η \frac{∂E}{∂W} \)
上の式の、\(\frac{∂E}{∂W}\)の計算をするにあたって、誤差逆伝播法を使用している。

「パラメータの更新を勾配法を用いて行うのだが、その際計算が大変複雑なので、それを誤差逆伝播法を用いて計算している」という理解です。

では、具体的にどの様に誤差逆伝播法を使って\(\frac{∂E}{∂W}\)を計算するのか見ていきます。

3. 計算に必要な知識

先に述べた様に、誤差逆伝播法は微分の計算方法になります。
なので、基本的に微分を使用していくのですが、特に偏微分と連鎖率を用いて進めていきます。

本章で、簡単に上記2つを解説します。

偏微分

偏微分は、変数が複数ある関数を微分する時に用いられます。

一つの変数にのみ注目し、それ以外の変数を定数として扱います。

以下に例を示します。

\( h = 5x^3 + 2y^2 - 7 \)

上記式を、xで偏微分する時、yを定数として扱います。yが定数なので、結果は以下となります。

\( \frac{∂h}{∂x} = 15x^2 \)

同様に、yで偏微分する時、xを定数として扱うので、以下となります。

\( \frac{∂h}{∂y} = 4y \)

逆伝播の計算時、この考え方がすごく出てくるので、押さえておきます。

連鎖率

連鎖率とは、合成関数の微分を行う時に使用する計算式です。

本来合成関数から解説すべきですが、今回割愛させていただきます。
とにかく「こんな感じの計算をする」という部分の理解に絞って進めていきます。

理解しやすい様に、1変数→2変数→多変数という流れでみていきます。

1変数

まず、以下の関数を考えます。

\( y = f(u) \) \( u = g(x) \)

上記式の\(y\)は\(u\)の関数と言え、且つ、\(u\)は\(x\)の関数と言えます。
これは、\(y = f(g(x))\)とも書くことができます。

上記式について、\(y\)を\(x\)について微分する時、以下の様に表せます。

\( \frac{dy}{dx} = \frac{dy}{du} \times \frac{du}{dx} \)

具体例として、以下の式を考えます。

\( y = (3x^2 + 9)^4 \)

上記を\(y\)を\(x\)について微分する時、頑張って展開して解くことももちろんできますが、\(y = (3x^2 + 9)^4\)の\(3x^2 + 9\)を\(u\)として考えることもできます。

\( y = u^4 \) \( u = 3x^2 + 9 \)

上記式において、\(y\)を\(x\)について微分する時、以下の様に解くことができます。

\( \frac{dy}{dx} = \frac{dy}{du} \times \frac{du}{dx} \)
\( = 3(3x^2 + 9)^3 \times 6x \)

\(\frac{dy}{du} = 3u^3\)、\(\frac{du}{dx} = 6x\)なので、上記の様に計算することが可能です。

2変数

次に、以下の関数を考えてみます。

\( z = f(u, v) \) \( u = g(x, y) \) \( v = h(x, y) \)

上記式の\(z\)は\(u\)の関数と言え、且つ、\(u\)は\(x, y\)の関数と言えます。
また、\(z\)は\(v\)の関数とも言え、且つ、\(v\)は\(x, y\)の関数と言えます。
これは、\(z = f(g(x, y), h(x, y))\)とも書くことができます。

上記式について、\(z\)を\(x\)について微分する時、以下の様に表せます。

\( \frac{∂z}{∂x} = \frac{∂z}{∂u} \times \frac{∂u}{∂x} + \frac{∂z}{∂v} \times \frac{∂v}{∂x} \)

具体例として、以下の式を考えます。

\( z = (x^3 + y^4)\sin xy \)

上記を\(z\)を\(x\)について微分する時、頑張って展開して解くことももちろんできますが、\((x^3 + y^4)\)を\(u\)として、また\(\sin xy\)を\(v\)として考えることもできます。

\( z = u \times v \) \( u = x^3 + y^4 \) \( v = \sin xy \)

上記式において、\(z\)を\(x\)について微分する時、以下の様に解くことができます。

\( \frac{∂z}{∂x} = \frac{∂z}{∂u} \times \frac{∂u}{∂x} + \frac{∂z}{∂v} \times \frac{∂v}{∂x} \)
\( = \sin xy \times 3x^2 + (x^3 + y^4) \times y \cos xy \)

\(\frac{∂z}{∂u} = \sin xy\)、\(\frac{∂u}{∂x} = 3x^2\)、\(\frac{∂z}{∂v} = (x^3 + y^4)\)、\(\frac{∂v}{∂x} = y \cos xy\)なので、上記の様に計算することが可能です。

多変数

最後に、以下の関数を考えてみます。

\( z = f(u_1, u_2, u_3, ...) \) \( u_1 = g(x_1, x_2, x_3, ...) \) \( u_2 = h(x_1, x_2, x_3, ...) \) \( ... \)

上記式の\(z\)は\(u_1\)の関数と言え、且つ、\(u_1\)は\(x_1, x_2, x_3, ...\)の関数と言えます。
また、\(z\)は\(u_2\)の関数とも言え、且つ、\(u_2\)は\(x_1, x_2, x_3, ...\)の関数と言えます。
さらに、\(z\)は\(u_3\)の関数とも言え、且つ、\(u_3\)は\(x_1, x_2, x_3, ...\)の関数と言えます。
これは、\(z = f(g(x_1, x_2, x_3, ...), h(x_1, x_2, x_3, ...), ...)\)とも書くことができます。

上記式について、\(z\)を\(k\)番目の\(x\)について微分する時、以下の様に表せます。

\( \frac{∂z}{∂x_k} = \frac{∂z}{∂u_1} \times \frac{∂u_1}{∂x_k} + \frac{∂z}{∂u_2} \times \frac{∂u_2}{∂x_k} + \frac{∂z}{∂u_3} \times \frac{∂u_3}{∂x_k}... \)

上記式をシグマを使って表します。

\( \frac{∂z}{∂x_k} = \sum_{i} \frac{∂z}{∂u_i} \times \frac{∂u_i}{∂x_k} \)

左辺の\(\frac{∂z}{∂x_k}\)の部分、なんとなく\(\frac{∂E}{∂W_k}\)っぽい感じがしないでしょうか。

実際、最適なWたちの値を判別する際、必ず多変数の微分が必要になります。
そして各関数たちは、他の層の関数に依存している関係となっています。

それらを計算する為に、この連鎖率を使用してWを最適化しています。

頻繁に出てくるので、ここで押さえておきます。

4. 設定

本章では、計算を行う上での設定を確認します。

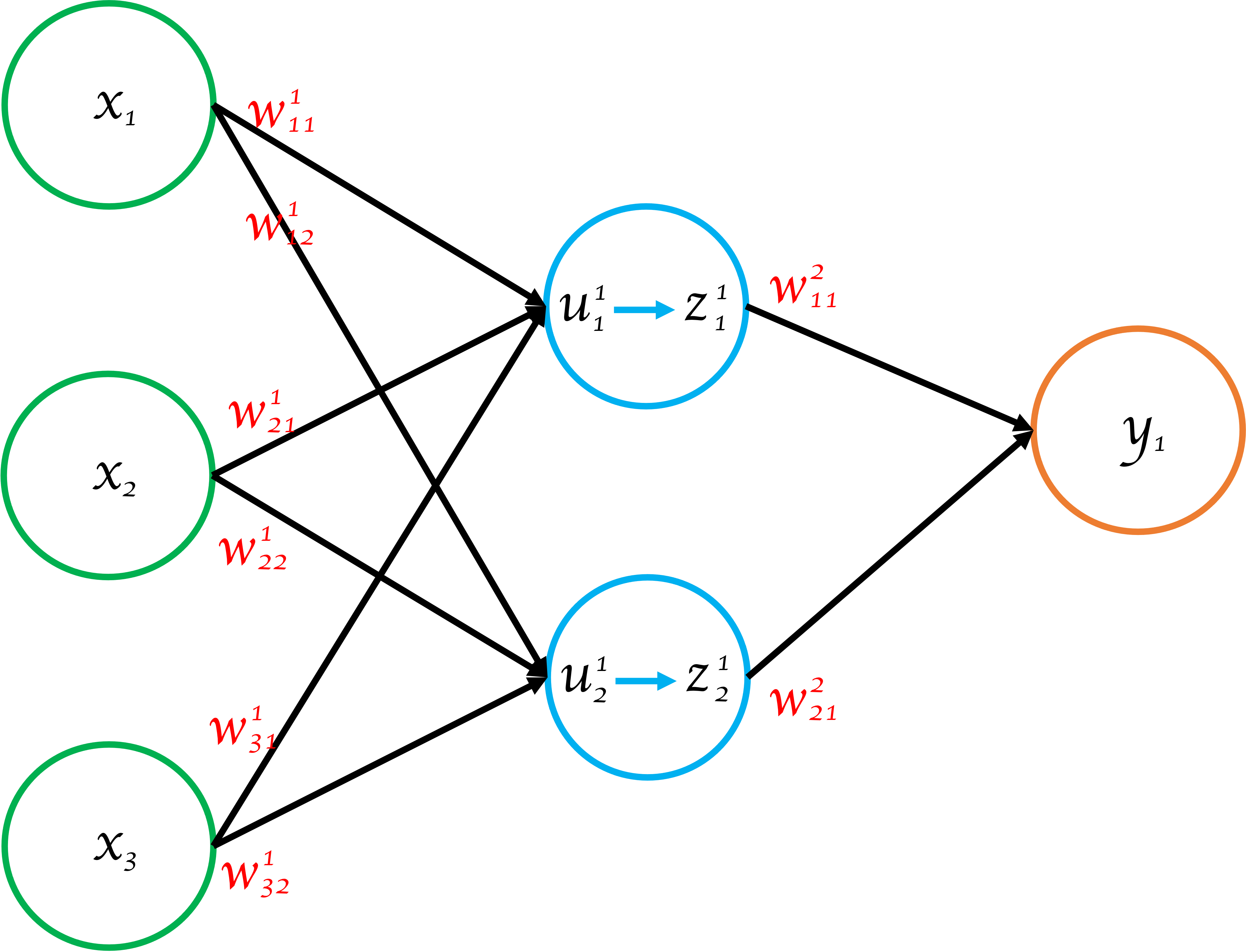図1　ニューラルネットワーク

図1はあるニューラルネットワークを図示したものです。

以下に図1の具体的記号の説明や各関数の設定を示します。

表1　各記号の説明と各関数の設定
記号 説明1 説明2
\(x\) 入力値 \(x_2\)の場合、2番目の入力値\(x\)を指す
\(z^l_j\) 出力値 重み付き線形和\(u\)を活性化関数に通した値のこと
\(z^3_2\)の場合、3層目で2番目の\(z\)を指す
\(z^L_j, y_j\) 出力層の出力値 -
\(w^l_{ij}\) 重み \(w^2_{23}\)の場合、\(z^1_{2}\)から\(z^2_{3}\)へ向かう重みを指す
\(u^l_j\) 重み付き線形和 前層のノードからの入力に重みを掛けて、全て足し合わせたもの
\(u^l_j = w^l_{0j}z^{l-1}_0 + w^l_{1j}z^{l-1}_1 + w^l_{2j}z^{l-1}_2 ...\)とする
\(t\) 正解値 \(y\)に対応しており、\(y_j\)に対応する値は\(t_j\)
\(f()\) 活性化関数 ここでは活性化関数 = 恒等関数を使用する
\(f(u) = u\)
※　恒等関数は、入力値を何も変更せず出力する関数のこと。
例えば、\(f(5) = 5\)となる
\(E\) ロス関数 ここではロス関数に以下の2乗誤差関数を使用する
\(E = \frac{1}{2}\sum_i(y_i - t_i)^2\)
\(η\)(イータ) 学習率 ここでは\(η = 0.001\)とする

上記をもとに、誤差逆伝播の計算を進めていきます。

5. 誤差逆伝播法の計算

では、実際に計算をしていきます。

まず、出力層のWとそれ以外のWで計算を分けます。それらは計算方法が異なる為です。

最初に、出力層におけるW変化量を計算します。その後、出力層から一つ手前の層の出力層におけるW変化量を計算し、さらにその後、もう一つ手前、、、というように、出力層から入力層に向かってWの変化量を計算していきます。

この理由は、先述した様に、ある重みWの変化が、後続のニューラルネットワークの値に影響を与えてしまうことにあります。
これを避ける為、後続がない出力層から計算を進め、1層ずつ手前（入力層側）に向かって計算を進めていきます。

これが誤差逆伝播法の「逆」の由来になります。

また、おさらいですが、Wを更新する式は以下になります。

式1

\( W = W + ΔW \)

ここで、ある１つの重みに注目します。設定より、以下の様に表せます。

式2

\( w^l_{ij} = w^l_{ij} + Δw^l_{ij} \)
\( Δw^l_{ij} = -η \frac{∂E}{∂w^l_{ij}} \)

誤差逆伝播法によって求めるのはここです。この式を求めることが目的となります。

\( Δw^l_{ij} = -η \frac{∂E}{∂w^l_{ij}} \)

では進めていきます。

出力層の\(Δw\)の計算

出力層の\(w\)(\(w^L_{ij}\))について、以下の式を計算します。

式3

\( Δw^L_{ij} = -η \frac{∂E}{∂w^L_{ij}} \)

\(\frac{∂E}{∂w^L_{ij}}\)に注目します。連鎖率を使用し、以下の様にします。

式4

\( \frac{∂E}{∂w^L_{ij}} = \frac{∂E}{∂u^L_j} \times \frac{∂u^L_j}{∂w^L_{ij}} \)

\(∂u^L_j\)が出てきました。

ロス関数\(E\)は重み付き線形和\(u\)の関数となっており、且つ、\(u\)は重み\(w\)の関数となっています。
\(E(u^L(w^L))\)ともかけます。

従って、式4の様に連鎖率で表すことが可能になっています。

関数の関係性については、図1をみていただくと分かりやすいと思います。

※　式4において、多変数の連鎖率なのに\(Σ\)が入っていないのは、今回\(W^L_{ij}\)に注目しており、それに影響されるのは\(u^L_j\)のみであるからです。

\(\frac{∂E}{∂u^L_j} = δ^L_j\)(デルタ)とおきます。因みに、この\(δ\)を「誤差」といいます（説明は後述）。

式5

\( \frac{∂E}{∂w^L_{ij}} = δ^L_j \times \frac{∂u^L_j}{∂w^L_{ij}} \)

\(\frac{∂u^L_j}{∂w^L_{ij}}\)は実は計算可能で、\(z^{L-1}_i\)となります。以下にその理由を示します。

まず、\(u^L_j\)を表すと、以下になります。

\( u^L_j = w^L_{11} \times z^{L-1}_1 + w^L_{21} \times z^{L-1}_2 +... \) \( + w^L_{ij} \times z^{L-1}_i + w^L_{i+1j} \times z^{L-1}_{i+1} + ... \)

ここで、\(\frac{∂u^L_j}{∂w^L_{ij}}\)を考えた時、偏微分なので、\(w^L_{ij} \times z^{L-1}_i\)のみが残ります。他は定数とみなすので全て落ちます。

よって、\(\frac{∂u^L_j}{∂w^L_{ij}}\)を計算すると、\(z^{L-1}_i\)となります。

式6

\( \frac{∂u^L_j}{∂w^L_{ij}} = z^{L-1}_i \)

\(z^{L-1}_i\)はニューラルネットワーク内に出てくる数値(1つ前の層の出力)なので、これで完了です。

次に、\(δ^L_j\)を計算します。

\(δ^L_j\)は、以下の様に表すことができます。

式7

\( δ^L_j = \frac{∂E}{∂u^L_{j}} \)
\( = \frac{∂E}{∂z^L_{j}} \times \frac{∂z^L_{j}}{∂u^L_j} \)

この連鎖率は式4と同様の考え方です。さらに変形します。

まず式7の\(\frac{∂z^L_{j}}{∂u^L_j}\)に注目します。

分子\(∂z^L_j\)は活性化関数を通した後の数値ですが、今回活性化関数は恒等関数としているので、以下となります。

式8

\( z^L_j = u^L_j \)

式8より、以下となります。

式9

\( \frac{∂z^L_{j}}{∂u^L_j} = \frac{∂u^L_{j}}{∂u^L_j} = 1 \)

次に式7の\(\frac{∂E}{∂z^L_j}\)に注目します。

分母\(z^L_j\)は、出力層の出力値なので\(z^L_j = y_j\)と表せます。

式10

\( \frac{∂E}{∂z^L_j} = \frac{∂E}{∂y_j} \)

式10は、つまり「ロス関数\(E\)を、\(y_j\)で偏微分せよ」ということです。

ロス関数Eは\(E = \frac{1}{2}\sum_i(y_i - t_i)^2\)です。

\(i\)の分だけ\((y - t)\)がありますが、今回注目するのは\((y_j - t_j)\)のみです。残りは定数とみなすので落ちます。

従って、以下となります。

式11

\( \frac{∂E}{∂y_j} = y_j - t_j \)

\(y_j\)と\(t_j\)はニューラルネットワーク内に存在する数値なので、それらを持ってくれば良いです。

結果的に、式7（\(δ^L_j\)）は以下の様に表せます。

式12

\( δ^L_j = y_j - t_j \)

これで必要な式は出揃いましたので、まとめます。

式5に、式6と式12を代入します。

式13

\( \frac{∂E}{∂w^L_{ij}} = δ^L_j \times \frac{∂u^L_j}{∂w^L_{ij}} \)
\( = (y_j - t_j) \times z^{L-1}_i \)

式3に、式13を代入します。

式14

\( Δw^L_{ij} = -η \frac{∂E}{∂w^L_{ij}} \)
\( = -η \times (y_j - t_j) \times z^{L-1}_i \)

これで、出力層の\(Δw\)の計算が完了しました。

非常に単純な計算式となりました。値も全てニューラルネットワーク内に存在する値なので、当然計算可能です。

ちなみに、\(δ^L_j\)は\(y_j - t_j\)となりました。まさに「誤差」ですよね。
次の出力層以外の計算時、この\(δ\)、つまり「誤差」が重要になってきます。

出力層以外の\(Δw\)の計算

出力層の\(w\)を\(w^l_{ij}\)とします。以下の式を計算します。

式15

\( Δw^l_{ij} = -η \frac{∂E}{∂w^l_{ij}} \)

\(\frac{∂E}{∂w^l_{ij}}\)に注目します。連鎖率を使用し、以下の様にします。

式16

\( \frac{∂E}{∂w^l_{ij}} = \frac{∂E}{∂u^l_j} \times \frac{∂u^l_j}{∂w^l_{ij}} \)

\(\frac{∂E}{∂u^l_j} = δ^l_j\)(デルタ)とおきます。

式17

\( \frac{∂E}{∂w^l_{ij}} = δ^l_j \times \frac{∂u^l_j}{∂w^l_{ij}} \)

\(\frac{∂u^l_j}{∂w^l_{ij}}\)を計算します。

出力層と同じ様に、\(z^{l-1}_i\)となります。

式18

\( \frac{∂u^l_j}{∂w^l_{ij}} = z^{l-1}_i \)

ここまでは、出力層の計算と同じです。
ここから先、\(δ^l_j\)の計算が先ほどとは違ってきます。

ということで、\(δ^l_j\)を計算していきます。

\(δ^l_j\)を以下の様に表します。

式19

\( δ^l_j = \frac{∂E}{∂u^l_j} \)
\( = \sum_k \frac{∂E}{∂u^{l+1}_k} \times \frac{∂u^{l+1}_k}{∂u^l_j} \)

出力層になかったシグマがつきました。
理由は、\(u^l_j\)は、仮に値が変わったとしたら、その次の層の\(u^{l+1}_1\), \(u^{l+1}_2\), \(u^{l+1}_3\)...も全て値が変わります。つまり影響をうけます。
従って、全て足し合わせる必要があります。

出力層の時と今回とで、シグマの有無に注意が必要です。

式19の\(\frac{∂E}{∂u^{l+1}_k}\)を\(δ^{l+1}_k\)とおきます。
さらに、\(\frac{∂u^{l+1}_k}{∂u^l_j}\)を次の様に変形します。

式20

\( δ^l_j = \frac{∂E}{∂u^l_j} \)
\( = \sum_k δ^{l+1}_k \times \frac{∂u^{l+1}_k}{∂z^l_j} \times \frac{∂z^l_j}{∂u^l_j} \)

式20について1つずつみていきます。

まず、\(\frac{∂u^{l+1}_k}{∂z^l_j}\)は結果的に\(w^{l+1}_{jk}\)と表すことが可能です。

理由として、まず\(u^{l+1}_k\)を考えます。
これは、重み付き線形和\(u\)の、\(l+1\)層目のものです。
\(...+...+ w^{l+1}_{jk} z^l_j + ...\)となっています。

この\(u^{l+1}_k\)を\(z^l_j\)で偏微分すると、\(w^{l+1}_{jk} z^l_j\)以外は定数とみなす為落ちます。
\(w^{l+1}_{jk} z^l_j\)のみと考えるので、結果\(w^{l+1}_{jk}\)となります。

次に、\(\frac{∂z^l_j}{∂u^l_j}\)は結果的に\(\frac{∂f^l(u^l_j)}{∂u^l_j}\)となります。

理由は、\(z^l_j\)は\(z^l_j = f(u^l_j)\)であるから、 \(\frac{∂z^l_j}{∂u^l_j} = f^{l'}(u^l_j)\)となります。つまり、単純に\(u^l_j\)についての微分となります。

更に、今回活性化関数\(f\)は恒等関数（\(f(x) = x\)）なので、微分すると\(f'(x) = 1\)となります。
よって\(\frac{∂z^l_j}{∂u^l_j} = 1\)となります（今回はそのまま\(\frac{∂z^l_j}{∂u^l_j} = \frac{∂f^l(u^l_j)}{∂u^l_j}\)としておきます）。

最後に、\(δ^{l+1}_j\)は結論からいうともう値が出ています。

例えば、出力層の1つ手前の中間層を\(l\)層とすれば、\(l+1\)層は出力層です。
出力層の\(δ\)は\(δ^L_j\)、つまり\(y_j - t_j\)でした。

ということは、\(δ^{l+1}_j = δ^L_j = (y_j - t_j)\)となります。

それをもとに\(δ^l_j\)を算出していきます。

次に、もう1つ手前の中間層に行った場合、\(δ^{l+1}_j\)は今回算出した\(δ^l_j\)を使って計算していきます。

\(δ^L\)が分かれば\(δ^{L-1}\)が分かり、\(δ^{L-2}\)が分かり、\(δ^{L-3}\)... 最終的に\(δ^1\)が分かります。

この様に、出力層から入力層へ\(δ\)を伝播させていきます。

因みに、\(δ^L_j = y_j - t_j\)(誤差)であり、それが逆方向へ伝播していくから「誤差逆伝播法」と呼ばれます。

これで必要な式は出揃いましたので、まとめます。

式17に式18と式20を代入します。

式21

\( \frac{∂E}{∂w^l_{ij}} = δ^l_j \times \frac{∂u^l_j}{∂w^l_{ij}} \)
\( = \sum_k δ^{l+1}_k \times w^{l+1}_{jk} \times \frac{∂f^l(u^l_j)}{∂u^l_j} \times z^{l-1}_i \)

式15に式21を代入します。

式22

\( Δw^l_{ij} = -η \frac{∂E}{∂w^l_{ij}} \)
\( = -η \sum_k δ^{l+1}_k \times w^{l+1}_{jk} \times \frac{∂f^l(u^l_j)}{∂u^l_j} \times z^{l-1}_i \)

計算まとめ

まとめます。

出力層の\(Δw\)の計算

\( Δw^L_{ij} = -η \times (y_j - t_j) \times z^{L-1}_i \)

出力層以外の\(Δw\)の計算

\( Δw^l_{ij} = -η \sum_k δ^{l+1}_k \times w^{l+1}_{jk} \times \frac{∂f^l(u^l_j)}{∂u^l_j} \times z^{l-1}_i \)

6. まとめ

今回はニューラルネットワークの学習における、誤差逆伝播法について解説しました。

次回も是非みてみてください！

7. 参考文献

斎藤康毅　著　「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」

・物体検出AIの導入
・アノテーションサービス
・手書き計算サイト ZONE++ の運営
・技術ブログ LAB++の運営
   上記をメインにおこなっております

詳しくはこちら

Category

Link

Search

Archives