【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.14】ニューラルネットワークの実装(weight decay)
1. 本記事について
本記事は、これまでの内容（ニューラルネットワークの理解その1〜4）を踏まえ、ニューラルネットワークをpythonプログラムに落とし込んでいきます。
本記事はこれまで実装してきた処理を使用して、簡単なニューラルネットワーク（NN）を実装していきます。
（前回は、重みの初期値について解説しました。）
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. weight decayについて
weight dacayとは
>weight decayとは、一言でいうと「過学習を抑える仕組み」と言えます。
ニューラルネットワークでは多層になればなるほど、そのモデルの表現能力が増します。しかし、多層になるほど過学習のリスクも高くなります。
モデルの表現能力を維持したまま、大きな重みに対してペナルティを与えることで過学習のリスクを減らすことが行われます。その手法の一つがweight decay(重み減衰)です。
YOLOv1でもweight decayが採用されているので、本記事で押さえておきます。
weight dacayの計算
具体的な計算方法ですが、ロス関数に\(\frac{1}{2}λW^{2}\)を足します。
ここでのロス関数はSSE（2乗和誤差）にします。
式1
\(W^{2}\)は、すべての重みの2乗の総和です。重みの値が大きいと損失関数の値も大きくなるようになっています。これを「ペナルティ」と表現しています。
大きな重みに対して、より大きなペナルティが課されるということになります。
逆伝播の時は、\(λW\)が伝播されます。
なぜ\(λW\)になるか説明します。Wを更新する式は以下です。
式2
ここで、ある１つの重みに注目します。
式3
式3の\(-η\frac{∂E}{∂w_{ij}^{l}}\)を解くのですが、ηは学習率で、簡便化のために\(η=1\)とします。
また、式1のロス関数で、\(\frac{1}{2}\sum_{k=1}^{n}{(y_k - t_k)^2}\)の部分もいったん無視し、weight decayの部分のみ（\(\frac{1}{2}λW^{2}\)）とします。
上記を踏まえると、以下になります。
式4
先ほどの通り、\(W^{2}\)は、すべての重みの2乗なので、以下と表せます。
式5
式5で、\(w_{ij}^{l}\)についての偏微分ですので、\(w_{ij}^{l}\)以外は落ちます。
なので、結果的に\(w_{ij}^{l}\)のみが残ります。
式6
式6のマイナスは、WからΔWを引いて更新するので、実質のΔWはλWとなります。
上記より、逆伝播の際はλWを使用します。
weight decayの注意点
実は、式1の\(\frac{1}{2}λW^{2}\)はL2正則化という、別の過学習を抑える仕組みと同一となっています。
そして、上記の計算は、重みの更新方法がSGD（\(W \leftarrow W - ΔW\)）の場合に限り適応されます。
ややこしいのですが、要は「上記の計算式は、重みの更新方法がSGDの時に限り有効」となります。
weight decayは、本来「ある層の重みを更新する際に、そのひとつ前の層の重みの一部を減算する」処理です。
それが、SGDに限っては、実装するとL2正則化と同じ処理になるという形です。
逆を言うと、SGD以外の重み更新手法では、式1をweight decayとして実装することは誤りと言えます。ここは注意が必要です。
weight decayの実装
では、実際にweight decayを実装していきます。
すでに実装した3層の全結合ニューラルネットーワーククラス「NeuralNetwork1」で、loss_func()とgradient()に、weight decayの処理をつけ足します。
def loss_func(self, x, t):
weight_decay = 0
for idx in range(3):
W = self.params['W' + str(idx+1)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.loss.forward(x, t) + weight_decay
def gradient(self):
dout = self.loss.backward()
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
self.grads['W1'] = self.layers['Affine1'].dW + self.weight_decay_lambda * self.layers['Affine1'].W
self.grads['b1'] = self.layers['Affine1'].db
self.grads['W2'] = self.layers['Affine2'].dW + self.weight_decay_lambda * self.layers['Affine2'].W
self.grads['b2'] = self.layers['Affine2'].db
self.grads['W3'] = self.layers['Affine3'].dW + self.weight_decay_lambda * self.layers['Affine3'].W
self.grads['b3'] = self.layers['Affine3'].db
return self.grads
loss_func()で、各層のWの2乗を足しています。そして、それらをすべて足し合わせていきます。
最後に、加算したweight_decayをロス値に足して返しています。
gradient()で、各層のdWにWを足しています。
クラスにまとめます。
# ３層の全結合NN
class NeuralNetwork1:
def __init__(self):
# 重み・バイアスの初期化
weight_init_std = 0.01
self.params = {}
self.grads = {}
self.weight_decay_lambda = 0
self.params['W1'] = weight_init_std * np.random.randn(784, 500)
self.params['b1'] = np.zeros((1, 500))
self.params['W2'] = weight_init_std * np.random.randn(500, 100)
self.params['b2'] = np.zeros((1, 100))
self.params['W3'] = weight_init_std * np.random.randn(100, 3)
self.params['b3'] = np.zeros((1, 3))
# 中間層の構築
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['LeakyReLU1'] = LeakyReLU(0.1)
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['LeakyReLU2'] = LeakyReLU(0.1)
self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])
self.loss = loss()# ロス関数
self.update = Momentum()# 更新関数
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss_func(self, x, t):
weight_decay = 0
for idx in range(3):
W = self.params['W' + str(idx+1)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.loss.forward(x, t) + weight_decay
def gradient(self):
dout = self.loss.backward()
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
self.grads['W1'] = self.layers['Affine1'].dW + self.weight_decay_lambda * self.layers['Affine1'].W
self.grads['b1'] = self.layers['Affine1'].db
self.grads['W2'] = self.layers['Affine2'].dW + self.weight_decay_lambda * self.layers['Affine2'].W
self.grads['b2'] = self.layers['Affine2'].db
self.grads['W3'] = self.layers['Affine3'].dW + self.weight_decay_lambda * self.layers['Affine3'].W
self.grads['b3'] = self.layers['Affine3'].db
return self.grads
def update_func(self):
self.update.update(self.params, self.grads)
__init__に、self.weight_decay_lambdaを追加しています。ここにλの値を指定します。
まずは、λ=0として、weight decayを使用せずに実行してみます。
最後に、一連の処理を実装してみます。
今回、過学習に対するweight decayの効果を見たいので、わざと過学習を起こすようにします。
学習に使うデータ数を減らし、それを何回も学習します。そうすることで、特定のデータに対してのみ過度に適応するようになります。
処理の最後に、学習データと検証データとでlossのグラフを描画し、差を確認します。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# 訓練データと検証データを取得
train_dataset = torchvision.datasets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
#download=True
download=False
)
test_dataset = torchvision.datasets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor(),
#download=True
download=False
)
# 0, 1, 2のみを抽出。及び教師データをone-hotベクトル化
train_box = []
for i, data in enumerate(train_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
train_box.append((t1, t2))
if len(train_box) == 100:# 過学習を起こすために、データ数を少なくしている
break
test_box = []
for i, data in enumerate(test_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
test_box.append((t1, t2))
if len(test_box) == 3000:
break
nn = NeuralNetwork1()# ネットワークをインスタンス化
# 学習（わざと過学習を起こす）
idx = 0
train_loss_list = []
test_loss_list = []
for _ in range(30):
for data_train in train_box:
data_test = test_box[idx]
x_train = data_train[0]
t_train = data_train[1]
x_test = data_test[0]
t_test = data_test[1]
# trainデータの学習
y_train = nn.predict(x_train)# 順伝播
loss_calc_train = nn.loss_func(y_train, t_train)# ロス
grads = nn.gradient()# 逆伝播→勾配計算
nn.update_func()# 重みの更新
# testデータの推論
y_test = nn.predict(x_test)# 順伝播
loss_calc_test = nn.loss_func(y_test, t_test)# ロス
if idx % 50 == 0:
train_loss_list.append(loss_calc_train)# リストに格納
test_loss_list.append(loss_calc_test)# リストに格納
if idx % 100 == 0:
print(f'train {idx+1}-{idx+100}...')
if idx % 200 == 0:
print(f'--loss_train: {loss_calc_train}')
print(f'--loss_test: {loss_calc_test}')
idx += 1
# lossの描画
vec = list(range(int(idx/50)))
plt.plot(vec, train_loss_list, label='train')
plt.plot(vec, test_loss_list, label='test')
plt.xlabel("epochs") # x軸ラベル
plt.ylabel("loss") # y軸ラベル
plt.title("LOSS", fontsize=20) # タイトル
plt.legend() # 凡例
plt.show()
以下実行結果です。
train 1-100...
--loss_train: 0.5002078471029034
--loss_test: 0.5018738339213634
train 101-200...
train 201-300...
--loss_train: 0.019563916798965866
--loss_test: 0.003081478029360385
train 301-400...
train 401-500...
...{省略}...
train 2601-2700...
--loss_train: 0.001277765880165811
--loss_test: 0.4382630346337104
train 2701-2800...
train 2801-2900...
--loss_train: 0.00043493250432250917
--loss_test: 0.004143508838610409
train 2901-3000...
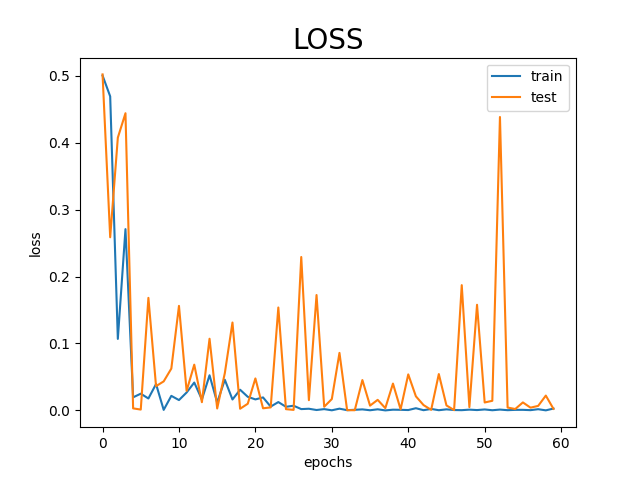図1 学習データと検証データのloss（weight decay 無し）
オレンジの線の検証データは、青い線の学習データに比べ、lossが下がりきっていない傾向です。
このモデルは、検証データという未知のデータに対して精度が低くなってしまっています。
次に、weight decayを使ってみます。
self.weight_decay_lambda = 0.1にして、同様の処理を実行してみます。
train 1-100...
--loss_train: 2.7029597343111083
--loss_test: 2.697614695905085
train 101-200...
train 201-300...
--loss_train: 0.2672519721073793
--loss_test: 0.4653690148290976
train 301-400...
train 401-500...
...{省略}...
train 2601-2700...
--loss_train: 0.21400536982071294
--loss_test: 0.7284580072485085
train 2701-2800...
train 2801-2900...
--loss_train: 0.21768825503500772
--loss_test: 0.21257823245189772
train 2901-3000...
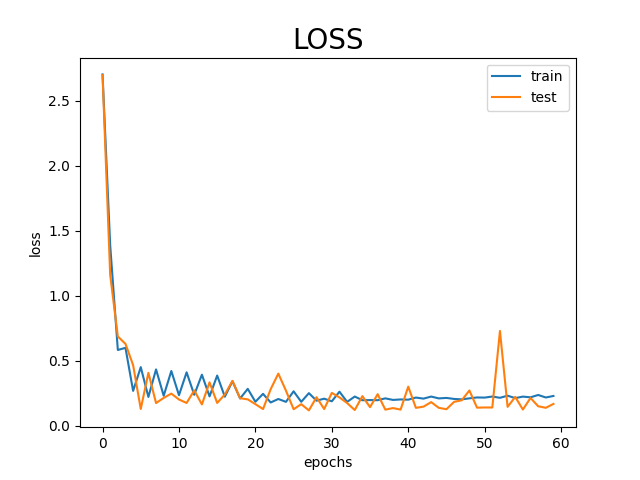図2 学習データと検証データのloss（weight decay 有り）
図1に比べ、オレンジの線と青い線の差がなくなっています。検証データという未知のデータに対しても適応できていることがわかります。
このように、weight decayは過学習を抑制する働きがあります。
YOLOv1では、λ=0.0005でweight decayを取り入れているので、本番の実装ではそのようにしたいと思います。
3. まとめ
今回はニューラルネットワークの実装（weight decay）について解説しました。
次回も是非みてみてください！
4. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search