【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.13】ニューラルネットワークの実装(重みの初期値)
1. 本記事について
本記事は、これまでの内容（ニューラルネットワークの理解その1〜4）を踏まえ、ニューラルネットワークをpythonプログラムに落とし込んでいきます。
本記事はこれまで実装してきた処理を使用して、簡単なニューラルネットワーク（NN）を実装していきます。
（前回は、３層のNN構築-学習と推論について解説しました。）
ニューラルネットワークの実装(入力層・Affine前半〜３層のNN構築-学習と推論)を見てから、本記事を見ることをお勧めします。
注意事項として、本シリーズではpythonの基礎的な解説、numpyの基礎的な解説は割愛させていただきます。特に、numpy配列やshape等頻出なので、その辺の知識が不十分の場合は、そちらの習得を先に行うことをお勧めします。
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. 重みの初期値について
今までの初期値
本シリーズでは、重みWの初期値にnp.random.randn()を使用してきました。これは平均が0、標準偏差が1になる正規分布、つまり標準正規分布に従う乱数を生成するモジュールです（正規分布についての詳細は割愛させていただきます）。
試しに3*10の乱数を生成してみます。
import numpy as np
W = np.random.randn(3, 10)
print(W)
[[-0.12544686 0.57144151 1.88362859 0.70056525 0.23098165 -0.99772044
-0.21884406 -0.45430165 1.08211236 -0.75986041]
[-1.89337295 0.04786452 -0.35648205 0.84824475 -1.96454444 -0.74182467
0.0921315 -2.10421522 -0.08645403 0.00844682]
[ 0.85481545 -0.3008695 -1.68461672 -0.19279451 -1.03557514 -0.07139938
-0.24212245 0.28209722 1.03226392 0.68117471]]
図で確認すると以下になります。数値を10000個生成します。
import numpy as np
W = np.random.randn(10000)
plt.hist(W, bins=50)
plt.show()
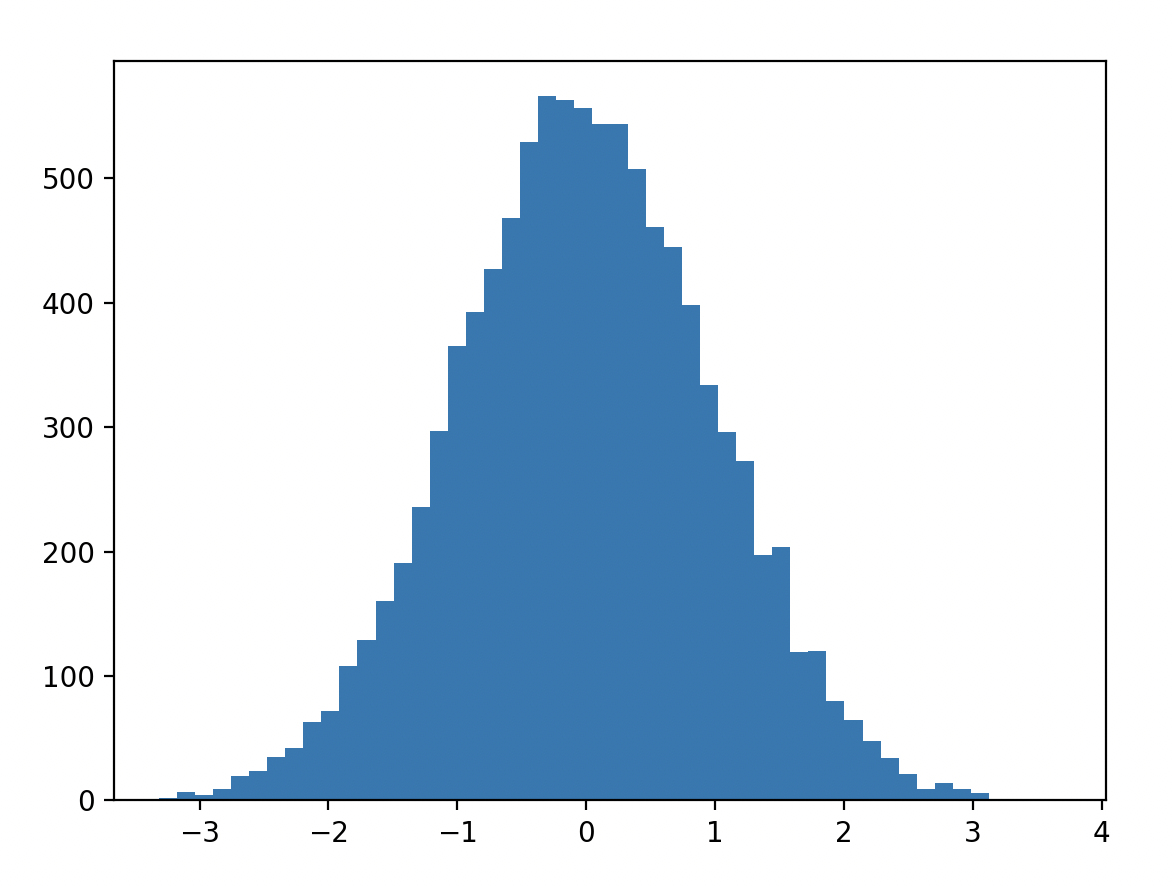図1 標準正規分布の図
統計などでよく見る図だと思います。
前回迄使用していたWは、これらに0.01を掛け、値を小さくしています。なぜかというと、前回実装したNNでいうと、0.01を掛けたほうが出力がいい感じになるからです。
前回で使用した３層のNNクラスについて、重みの初期化を0.01掛けで行っています。
試しに、0.01を外した場合の出力値とロスを確認します。
コードは前回で使用したものを踏襲し、weight_init_std = 1とします。
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# ３層の全結合NN
class NeuralNetwork1:
def __init__(self):
# 重み・バイアスの初期化
#weight_init_std = 0.01
weight_init_std = 1
self.params = {}
self.grads = {}
self.params['W1'] = weight_init_std * np.random.randn(784, 500)
self.params['b1'] = np.zeros((1, 500))
self.params['W2'] = weight_init_std * np.random.randn(500, 100)
self.params['b2'] = np.zeros((1, 100))
self.params['W3'] = weight_init_std * np.random.randn(100, 3)
self.params['b3'] = np.zeros((1, 3))
# 中間層の構築
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['LeakyReLU1'] = LeakyReLU(0.1)
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['LeakyReLU2'] = LeakyReLU(0.1)
self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])
self.loss = loss()# ロス関数
self.update = Momentum()# 更新関数
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss_func(self, x, t):
return self.loss.forward(x, t)
def gradient(self):
dout = self.loss.backward()
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
self.grads['W1'] = self.layers['Affine1'].dW
self.grads['b1'] = self.layers['Affine1'].db
self.grads['W2'] = self.layers['Affine2'].dW
self.grads['b2'] = self.layers['Affine2'].db
self.grads['W3'] = self.layers['Affine3'].dW
self.grads['b3'] = self.layers['Affine3'].db
return self.grads
def update_func(self):
self.update.update(self.params, self.grads)
# 訓練データと検証データを取得
train_dataset = torchvision.datasets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
#download=True
download=False
)
test_dataset = torchvision.datasets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor(),
#download=True
download=False
)
# 0, 1, 2のみを抽出。及び教師データをone-hotベクトル化
train_box = []
for i, data in enumerate(train_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
train_box.append((t1, t2))
if len(train_box) == 5000:
break
test_box = []
for i, data in enumerate(test_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
test_box.append((t1, t2))
if len(test_box) == 20:
break
nn = NeuralNetwork1()# ネットワークをインスタンス化
for i, data in enumerate(train_box):
x = data[0]
t = data[1]
y = nn.predict(x)# 順伝播
loss_calc = nn.loss_func(y, t)# ロス
print(f'y: {y}')
print(f'loss: {loss_calc}')
print()
if i == 4:
break
y: [[-4248.71146093 956.09146874 -31.2839652 ]]
loss: 9487568.542132823
y: [[-1272.43415859 648.35073992 705.58568932]]
loss: 1268001.4166913137
y: [[-736.75252609 516.16927946 -96.94708595]]
loss: 409414.32070214767
y: [[-1806.40450696 2013.81330447 -182.42581711]]
loss: 3673896.910082736
y: [[-1811.8248297 1142.51821832 34.97224315]]
loss: 2293498.057035498
出力値、ロス共に非常に大きな値になってしまいました。この後の処理でオーバーフロー及びアンダーフローの元になりかねません。つまりあまり良い初期値でないということになります。
上記の様な数値にならない様に、最初に重みに0.01を掛けていい感じにしていたということです。
以上が、いままで使用してきた重みの初期値です。
次に「Heの初期値」を解説します。
Heの初期値
Heの初期値について解説する前に、0.01掛けのデメリットをお伝えします。
0.01掛けは、層があまり深くないネットワークでは有効ですが、層が深くなると出力値が偏ってしまう傾向があります。
試しに、６層の簡易ネットワークと、出力の結果を以下に示します。
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# 訓練データと検証データを取得
train_dataset = torchvision.datasets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
#download=True
download=False
)
test_dataset = torchvision.datasets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor(),
#download=True
download=False
)
# 0, 1, 2のみを抽出。及び教師データをone-hotベクトル化
train_box = []
for i, data in enumerate(train_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
train_box.append((t1, t2))
if len(train_box) == 5000:
break
test_box = []
for i, data in enumerate(test_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
test_box.append((t1, t2))
if len(test_box) == 20:
break
nn = NeuralNetwork1()# ネットワークをインスタンス化
def LeakyReLU(x):
return np.where(x > 0, x, 0.1*x)
activations = {}
x = train_box[0][0]
weight_init_std = 0.01
for i in range(6):
if i == 0:
w = weight_init_std * np.random.randn(784, 500)
elif i == 1:
x = activations[i-1]
w = weight_init_std * np.random.randn(500, 100)
elif i in (2, 3, 4):
x = activations[i-1]
w = weight_init_std * np.random.randn(100, 100)
else:
x = activations[i-1]
w = weight_init_std * np.random.randn(100, 3)
a = np.dot(x, w)# Affine順伝播の計算
z = LeakyReLU(a)# 活性化関数
activations[i] = z# 出力を保存
# 作図
for i, z in activations.items():
plt.subplot(1, len(activations), i+1)
plt.hist(z.flatten(), bins=30, range=(-0.5, 0.5))
plt.xticks([-0.5, 0.0, 0.5])
if i != 0:
plt.yticks([], [])
plt.title(str(i+1))
plt.show()
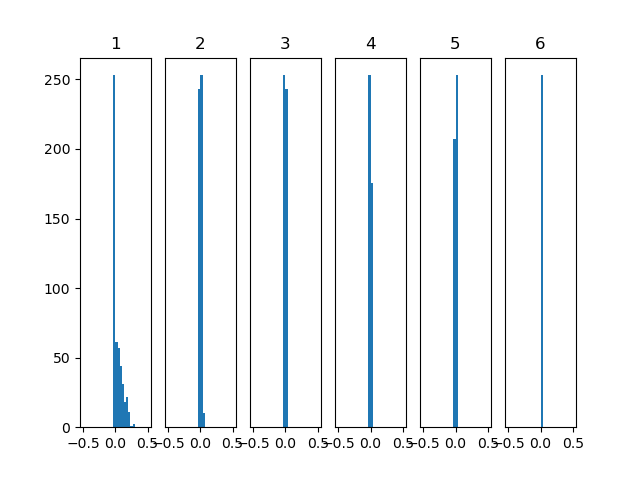図2 重みに0.01を掛けた際の出力
図2を見ると、２層目以降出力値が0.0付近に偏ってしまっているのがわかります。
これは、活性化関数がReLUの時に生じやすいです。理由としては、ReLUは負の数を0にして返すので、出力が0になる場合が多いためです。
今回活性化関数にLeaky ReLUを使用しています。Leaky ReLUも0近傍に出力が集中します。
この状態を回避するために、Heの初期値を使用します。
Heの初期値は、前層のノード数を\(n\)として、重みに\(\sqrt{\frac{2}{n}}\)を掛けます。
今回で言うと、１層目は\(n=784\)、２層目は\(n=500\)、３〜６層目は\(n=100\)となります。
先ほどの簡易ネットワークに、Heの初期値を取り入れてみます。
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# 訓練データと検証データを取得
train_dataset = torchvision.datasets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
#download=True
download=False
)
test_dataset = torchvision.datasets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor(),
#download=True
download=False
)
# 0, 1, 2のみを抽出。及び教師データをone-hotベクトル化
train_box = []
for i, data in enumerate(train_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
train_box.append((t1, t2))
if len(train_box) == 5000:
break
test_box = []
for i, data in enumerate(test_dataset):
if data[1] in (0, 1, 2):
t1 = data[0].numpy().copy().reshape(-1, 784)
t2 = np.eye(3)[data[1]]
test_box.append((t1, t2))
if len(test_box) == 20:
break
nn = NeuralNetwork1()# ネットワークをインスタンス化
def LeakyReLU(x):
return np.where(x > 0, x, 0.1*x)
activations = {}
x = train_box[0][0]
for i in range(6):
if i == 0:
w = np.sqrt(2 / 784) * np.random.randn(784, 500)
elif i == 1:
x = activations[i-1]
w = np.sqrt(2 / 500) * np.random.randn(500, 100)
elif i in (2, 3, 4):
x = activations[i-1]
w = np.sqrt(2 / 100) * np.random.randn(100, 100)
else:
x = activations[i-1]
w = np.sqrt(2 / 100) * np.random.randn(100, 3)
a = np.dot(x, w)# Affine順伝播の計算
z = LeakyReLU(a)# 活性化関数
activations[i] = z# 出力を保存
# 作図
for i, z in activations.items():
plt.subplot(1, len(activations), i+1)
plt.hist(z.flatten(), bins=30, range=(-0.5, 0.5))
plt.xticks([-0.5, 0.0, 0.5])
if i != 0:
plt.yticks([], [])
plt.title(str(i+1))
plt.show()
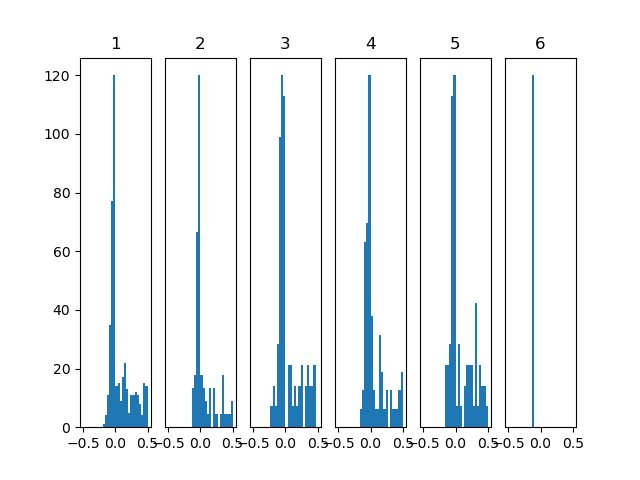図3 Heの初期値を使用した際の出力
図3を見ると、図2に比べ0の偏りが少なくなっており、その分ある程度分布が保たれていることがわかります。
図2では各層の重みに0.01を掛けていましたが、図3では１層目に\(\sqrt{\frac{2}{784}}\fallingdotseq0.0505\)、２層目に\(\sqrt{\frac{2}{500}}\fallingdotseq0.6325\)、３〜６層目に\(\sqrt{\frac{2}{100}}\fallingdotseq0.1414\)を重みに掛けています。
こうすることで、出力の偏りを抑えることができます。
因みに、Heの初期値は基本的に活性化関数がReLUの場合に有効とされています。
他には、活性化関数がシグモイドの場合はXavierの初期値というものを使用するのが有効とされています。
本シリーズでは活性化関数は基本的にLeaky ReLUを使用するので、初期値にHeの初期値を指定していきます。
3. まとめ
今回はニューラルネットワークの実装（重みの初期値）について解説しました。
次回も是非みてみてください！
4. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search