【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.6】ニューラルネットワークの実装(Affine後半)
1. 本記事について
本記事は、これまでの内容（ニューラルネットワークの理解その1〜4）を踏まえ、ニューラルネットワークをpythonプログラムに落とし込んでいきます。
本記事で中間層（逆伝播の残り）の実装を解説していきます。
（前回は、Affineの順伝播・逆伝播の途中迄（重み）解説しました。）
ニューラルネットワークの理解その1~4を見てから、本記事を見ることをお勧めします（特にその4）。
注意事項として、本シリーズではpythonの基礎的な解説、numpyの基礎的な解説は割愛させていただきます。特に、numpy配列やshape等頻出なので、その辺の知識が不十分の場合は、そちらの習得を先に行うことをお勧めします。
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. Affine層
順伝播
前回実装済み。
逆伝播
重み
前回実装済み。
バイアス
バイアスの実装から進めていきます。
ニューラルネットワークにおいて、重みWの値のみを更新すれば良いと思われがちですが、バイアスbも更新します。
bの更新量\(Δb\)については、計算も併せてここで解説します。
式1
\(ΔW\)の更新の計算とほぼ一緒です。
\(u^l_j\)を表すと、以下になります。
ここで、\(\frac{∂u^l_j}{∂b^l}\)を考えた時、偏微分なので、\(b^l\)のみが残ります。他は定数とみなすので全て落ちます。
よって、\(\frac{∂u^l_j}{∂b^l}\)を計算すると、\(1\)となります。
従って、\(\frac{∂E}{∂b^l}\)は\(δ^l_j\)のみが残ります。 添字を落として、以下の式で表します。
式2
ここで、
\(δ^l\)をdoutとします。
\(\frac{∂E}{∂b^l}\)をdbとします。
上記の条件で実装します。
import numpy as np
db = dout
非常にシンプルになりました。
具体例として、doutを以下とし、dbを算出してみます。
import numpy as np
# δ: ノード数３
dout = np.array([[0.71, 0.57, 0.35]])
db = dout
print(db)
print(dW.shape)
[[0.71 0.57 0.35]]
(1, 3)
dout（\(\frac{∂E}{∂b^l}\)）の値を元にbを更新していくことになります。
Affine層でのバイアスの計算は以上となります。
δ
dWとdbの他に、\(δ\)（正確にいうと\(δ^{l-1}\)）を計算する必要があります。
逆伝播を実装する際は、\(δ\)をreturnして出力する形となります。出力された\(δ\)が一つ前の層、つまり\(l-1\)層のdoutとして入力されます。
バイアス同様に、計算も確認していきます。
前回の重みの逆伝播の計算より、\(δ^l\)は以下の様に表すことができました。
式3
式3について、考えるポイントが3つあります。
1つ目に、\(\frac{∂f^l(u^l_j)}{∂u^l_j}\)についてです。
\(f^l()\)というのは活性化関数です。本実装ではAffineと活性化関数は別個に実装しようと思いますので、\(\frac{∂f^l(u^l_j)}{∂u^l_j}\)は今回無くします。
この部分は活性化関数の逆伝播の時に計算がなされる形となります。
例えば、\(l\)層のAffineで計算された\(δ\)は、\(l-1\)層の活性化関数へ伝播します。そこで\(δ\)の微分計算が行われ、\(l-1\)層のAffineに伝播される、というイメージです。
従って、\(δ\)の計算は以下となります。
式4
考えるポイント2つ目に、\(\sum_k\)の部分です。
\(\sum_k\)は、つまり全ての\(δ^{l+1} \times w^{l+1}\)の値を足しています。
この部分について、pythonで実装する際は足し合わせず、そのままの形（shape)を保持したまま計算を行っていきます。
python（numpy）は各配列の形状を保ったまま演算処理を行うことができます（余談ですが、ここがpythonと深層学習との相性がよい所以じゃないかと思います）。
従って、\(\sum_k\)を落として、以下の式で表します。
式5
考えるポイント3つ目に、\(δ^{l+1}\)と\(w^{l+1}\)いずれも\(l+1\)層目の値ということです。これはつまり、１つ出力側の層から逆伝播してきた値ということです。
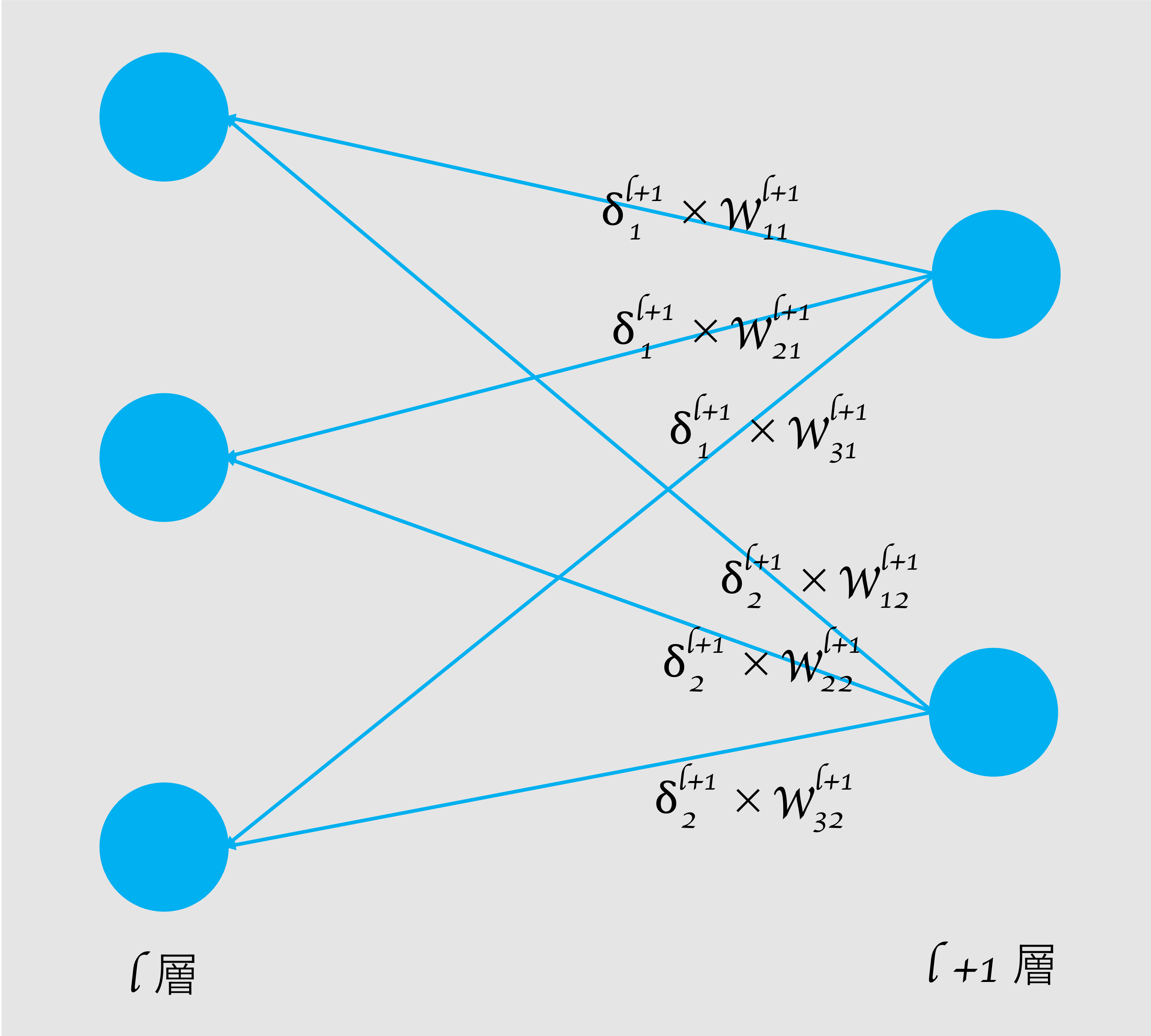図1 ニューラルネットワーク（逆伝播を図示）
\(l\)層での出力は、次の\(l-1\)層の入力となりますので、ややこしいですが、式で表すと以下になります。
式6
逆伝播されてきた値は、\(δ\)に\(w\)を乗算したものとなっています。ということは、今ここにいる層（=\(l\)層）でも同様に\(δ\)に\(w\)を乗算して、次（=\(l-1\)層）に渡してあげる必要があるという理屈です。
長くなりましたが、最終的に式6を逆伝播の出力としてpythonで実装します。
\(δ^{l-1}\)をdxとします。
\(δ^l\)をdoutとします。
\(w^l\)をWとします。
上記の条件で実装します。
import numpy as np
dx = np.dot(dout, W.T)
長々と解説してきましたが、pythonで実装すると１行で終わりです。
具体例として、Wとdoutをそれぞれ以下とし、dxを算出してみます。
import numpy as np
# 重み: 入力4 * 出力3
W = np.array([
[0.37, 0.52, 0.79],
[0.29, 0.83, 0.12],
[0.54, 0.77, 0.63],
[0.48, 0.29, 0.85]
])
# δ: ノード数３
dout = np.array([[0.71, 0.57, 0.35]])
dx = np.dot(dout, W.T)
print(dx)
print(dx.shape)
[[0.8356 0.721 1.0428 0.8036]]
(1, 4)
\(δ^{l-1}\)を変数dxとしましたが、これは、本記事冒頭でご紹介させていただいている書籍「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」に倣って命名しています。
変数名だけでなく、pythonで実装するにあたって、多分に参考にさせていただいている次第です。
上記書籍では、逆伝播の部分を「計算グラフ」という概念でわかりやすく解説されています。（計算グラフにおいて、ここでいう\(δ\)をxの勾配としてdxとしています）。
まだ未読の方がいらっしゃれば、是非お勧めですので、読んでみてください。
すいません、脱線してしまいましたが、以上で逆伝播の実装は完了です。逆伝播はそれぞれ重み・バイアス・\(δ\)の計算があり、少々複雑ですが、コードに落とすと数行で終わりです。
Affineまとめ
順伝播・逆伝播をそれぞれ１つのクラスにまとめます。
import numpy as np
class Affine:
# 各値の初期化
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
# 順伝播
def forward(self, x):
self.x = x # 順伝播の入力を保持
out = np.dot(x, self.W) + self.b
return out
# 逆伝播
def backward(self, dout):
dx = np.dot(dout, self.W.T) # δの計算
self.dW = np.dot(self.x.T, dout) # 重みの計算
self.db = dout # バイアスの計算
return dx
これでAffine層をpythonで実装完了しました。最後に、実際に数値を入れて動作を確認します。
import numpy as np
class Affine:
# 各値の初期化
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
# 順伝播
def forward(self, x):
self.x = x # 順伝播の入力を保持
out = np.dot(x, self.W) + self.b
return out
# 逆伝播
def backward(self, dout):
dx = np.dot(dout, self.W.T) # δの計算
self.dW = np.dot(self.x.T, dout) # 重みの計算
self.db = dout # バイアスの計算
return dx
### 実際に数値を入力してみる ###
# 入力: ノード数4
x = np.array([[0.24, 0.71, 0.19, 0.33]])
# 重み: 入力4 * 出力3
W = np.array([
[0.37, 0.52, 0.79],
[0.29, 0.83, 0.12],
[0.54, 0.77, 0.63],
[0.48, 0.29, 0.85]
])
# バイアス: ノード数3
b = np.array([[0.26, 0.42, 0.88]])
# δ: ノード数３
dout = np.array([[0.71, 0.57, 0.35]])
# インスタンス化
layer = Affine(W, b)
# 順伝播
Y = layer.forward(x)
print(Y)
print()
# 逆伝播
dX = layer.backward(dout)
print(dX)
print()
print(layer.dW)
print()
print(layer.db)
[[0.8157 1.3761 1.555 ]]
[[0.8356 0.721 1.0428 0.8036]]
[[0.1704 0.1368 0.084 ]
[0.5041 0.4047 0.2485]
[0.1349 0.1083 0.0665]
[0.2343 0.1881 0.1155]]
[[0.71 0.57 0.35]]
エラーなく処理できています。
3. まとめ
今回はニューラルネットワークの実装（Affine層）について解説しました。
次回も是非みてみてください！
4. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search