【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.2】ニューラルネットワークの理解(その2)
1. 本記事について
本記事はニューラルネットワークがどういったものかについて解説していきます。その1〜その4の4回を予定しており、本記事はその2です。
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. ロス関数について
ロス関数（損失関数と言ったりもします）とは、一言で言うと「推論値と正解値の差を求める関数」です。
差を求めてどうすんの？と思われるかもしれませんが、この差が非常に重要になってきます。
ニューラルネットワークは、この差を小さくする様に「学習」（＝重みやバイアスの値を最適化すること）をします。
学習するには、現状の推論値と正解値とでどれくらい差があるかを確認しなければいけないということです。その為に、「差」を算出することは非常に重要と言えます。
具体例をあげて解説します。
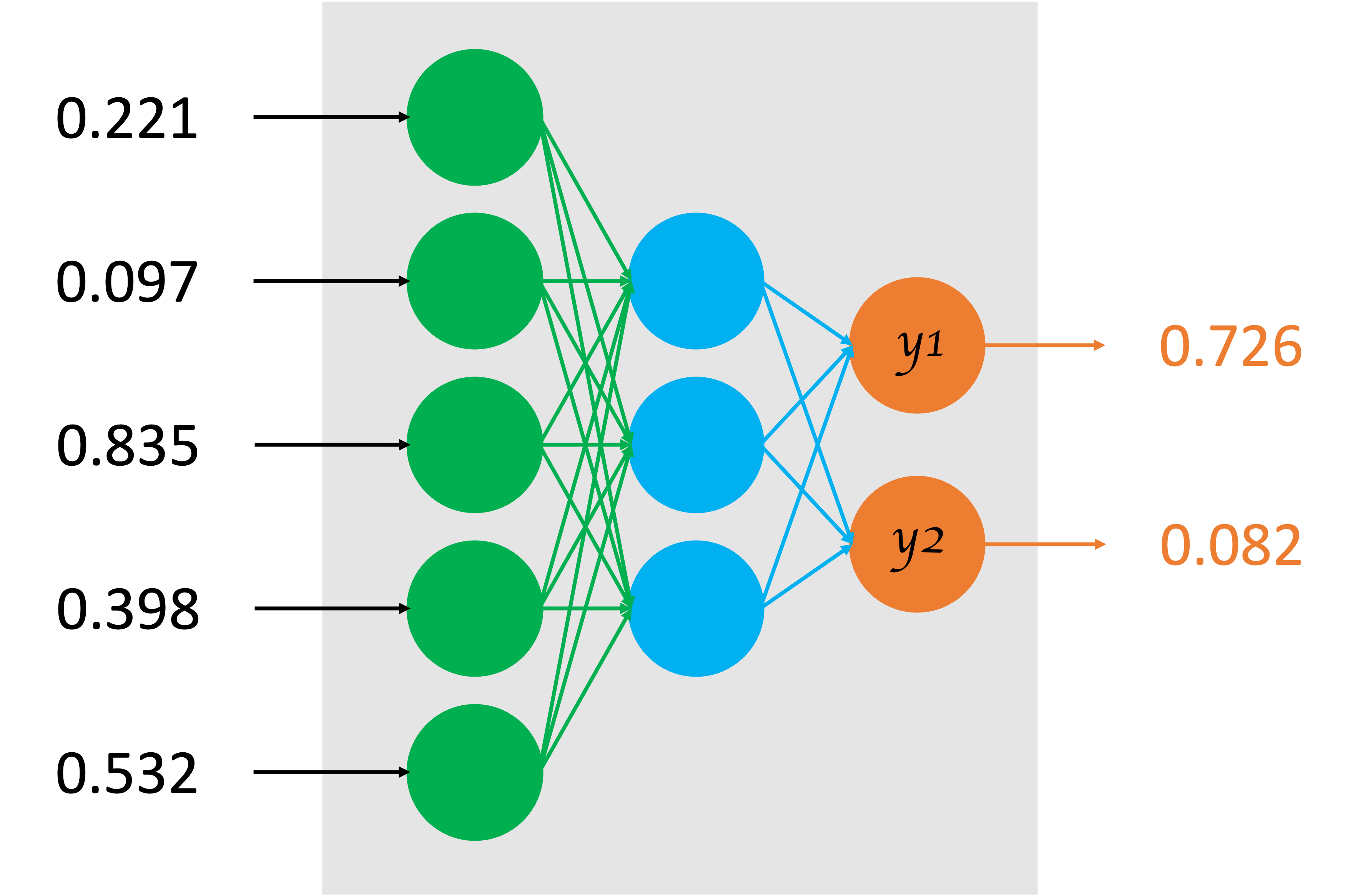図1 ニューラルネットワークの例
図1は、ある数値データをニューラルネットワークに入力した時の数値の流れを示しています。
5つの数値が入力層に渡され、中間層を経て、出力層へいきます。
その中で
前回解説した
計算が施され、\(y_1\)と\(y_2\)が算出されます。
図1では\(y_1=0.726\)、\(y_2=0.082\)となっています。
この2つの数値が、先述した推論値となります。
要は、今時点で、このモデルは[0.221, 0.097, 0.835, 0.398, 0.532]という数値データを入力すると、0.726と0.082の2つの数値が推論されるモデルであるといえます。
物体検出領域の場合、必ず推論値に対応する正解値が存在します。
\(y_1\)に対応する正解値を\(t_1\)とし、\(y_2\)に対応する正解値を\(t_2\)とします。そして、それぞれ\(t_1=0\)、\(t_2=1\)とします。
要は、\(y_1\)は今0.726ですが、最終的にはなるべく正解値である0に近づけたい。\(y_2\)は今0.082ですが、最終的にはなるべく正解値である1に近づけたいということです。
その為に、まず0.726と0がどの程度離れているか、0.082が1とどの程度離れているかを算出する必要があります。
その後、その数値をもとに重みの値とバイアスを変更していくことになります。
これが先述した「学習」と言うことになります(学習については次記事で解説予定です)。
ロス関数は、学習の前に、推論値と正解値がどの程度離れているかを算出する関数です。
3. ロス関数の計算
具体的に、推論値と正解値がどの程度離れているか、計算をしていきます。
最も手っ取り早いのは単純に引き算し、絶対値をとる方法です。
式1
ただ、この方法はあまり見かけません。
絶対値の計算は、プログラムに落とし込んだ時に煩雑になるので、大体差の2乗をとることが多いです。
式2
\(y_2\)も同様です。
式3
各差(ここでは\(e_1\)と\(e_2\))は、出力層のノードの数分存在します。ロス関数はそれらを全て足し合わせる必要があります。式にすると、以下の式になります。
式4
ここでは、出力層のノードの数が\(n\)個あるとしています。
このロス関数は2乗和誤差(Sum of Squared Error :SSE)と呼ばれ、頻繁に出てきます。
本シリーズで構築予定のYOLOv1におけるロス関数は、基本的に2乗和誤差で構築されています。
ロス関数Eを求めたら、その値を利用して重みとバイアスの値を更新していきます。
そしてまた推論をし、ロス関数を求め、また更新。。。その繰り返しでロス関数Eの値を小さくしていきます。
4. まとめ
今回はニューラルネットワークにおけるロス関数について、またロス関数の計算について解説しました。
次回も是非みてみてください！
5. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search