【フレームワークを使用せず】ゼロから作る物体検出AIモデル
【No.3】ニューラルネットワークの理解(その3)
1. 本記事について
本記事はニューラルネットワークがどういったものかについて解説していきます。その1〜その4の4回を予定しており、本記事はその3です。
本シリーズを進めていくにあたり、参考にさせていただく書籍があります。オライリー・ジャパンから出版されている「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」です。
本記事は、上記書籍を参考にさせていただいております。
2. ニューラルネットワークの学習について
ニューラルネットワークにおける学習とは、「重みやバイアスの値を最適化すること」といえます。
最適化するとは、端的に「ロス関数の値を小さくすること」です。言い換えると、学習とは、重みやバイアスの値を、ロス関数が小さくなる様な値に変更していくことです。
具体的に、ニューラルネットワークにおいて、どの様に重みやバイアスの値は決定されるのでしょうか。そのアルゴリズムをみていきます。
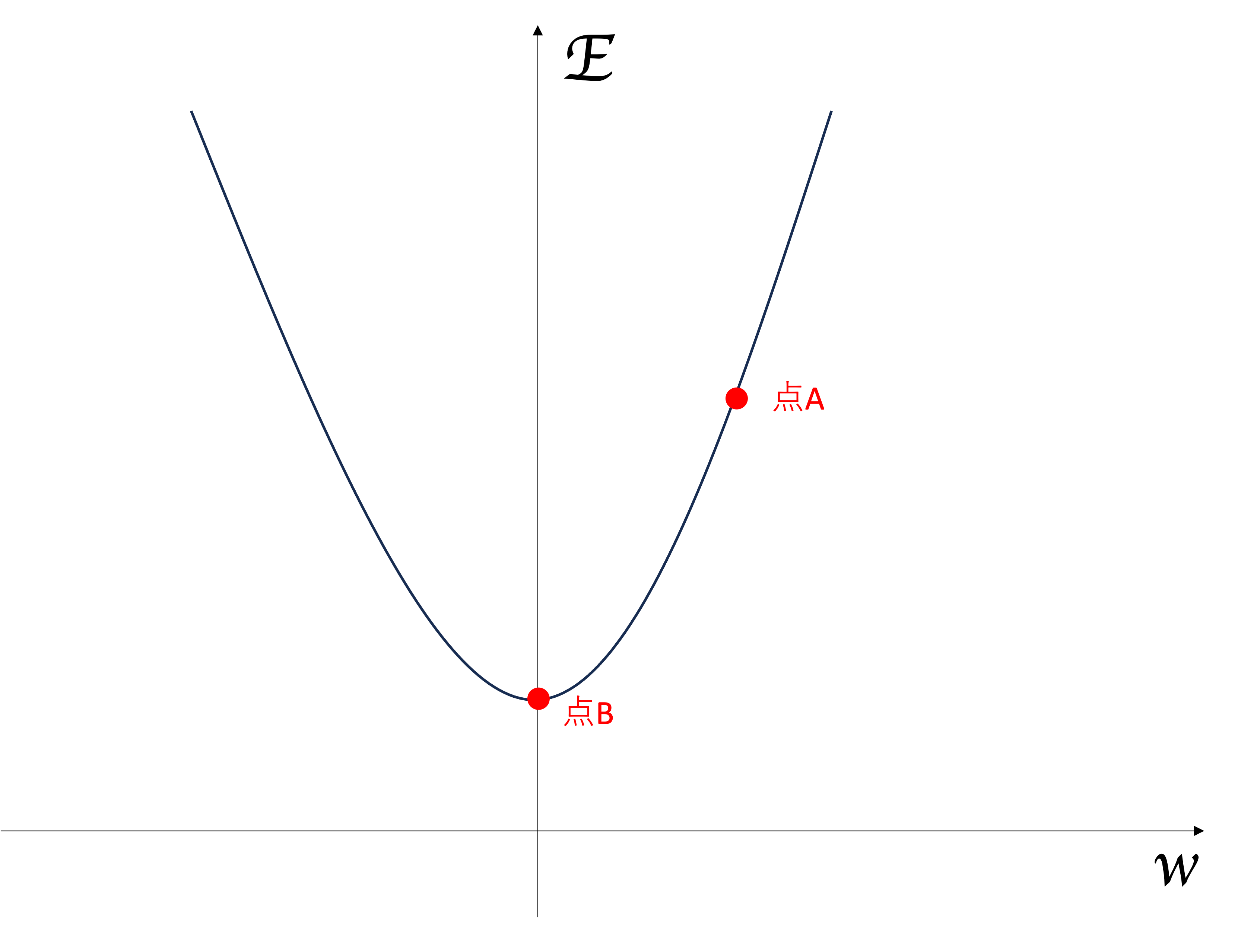図1 ロス関数と重みの関係性をグラフ化した図
図1は横軸を重みとバイアスの値（ここではWとします）、縦軸をロス関数の結果（ここではEとします）とした関数\(E(W)\)グラフです。
今、WとEの値はすでにわかっています。それらの値から、今我々は点Aにいます。
我々は、Eの値をなるべく下げたいと思っています。つまり、Eの値が最小になる点Bを目指すことになります。
この時、どの様にEが最小になる様なWの値を計算すれば良いでしょうか？ 答えは、「勾配法」という計算方法を用います。
3. 勾配法
勾配法の概要
図1に関して、わかりやすくする為に\(E(W)\)の関数を以下の様に仮定します。
式1
要は2次関数のグラフです。
今、我々は点Aにいます。点Aにおいて\(W=5\)とします。
この時、点Aを通る接線の傾き＝勾配を計算します。これが勾配法です。
具体的に点Aにおける勾配（点Aを通る接線の傾き）を求めます。
接線の傾きを計算するには、微分を使います（微分についての解説は割愛させていただきます）。
式1をWについて微分すると以下になります。
式2
今、点Aを通る接線の傾きを知りたいので、\(W=5\)を代入します。
式3
点Aにおける接線の傾きが10と求まりました。つまり、Aにおける勾配が10ということです。
次に、この勾配にある値を掛けてWの変化量を算出します。
ある値とは、学習率と呼ばれる値で、定数です。
数式では\(η\)（イータ）という記号で表されることが多いです。
ここでは\(η=0.001\)とします。
式4
\(ΔW\)はWの変化量を表します。これを元のWから引きます。今、\(W=5\)だったので、以下の様になります。
式5
これで、Wの更新が完了しました。元の5という値から、4.99という値に変わりました。
これは、0.01分点Bに近づいた形です。次はW=4.99を用いて出力値を出し、ロス関数に通し、上記の勾配法で変化量を計算し、Wを更新し、、、これを繰り返して少しずつEを少なくしていきます。
これが勾配法による重みの最適化というものになります。
勾配法の式を一般化すると、以下になります。
式6
\(ΔW\)がどの程度Wを変化させるかの変化量です。これはE(W)をWについて微分した値です。
そして、元のWからΔWを引くことで、Wの値を更新します。
以上が勾配法の概要になります。
ニューラルネットワークで勾配法を利用する
勾配法の中で、WとEの関数を\(E(W) = W^2 + 4\)としました。
この時のWは重みとバイアスの値としましたが、実際のニューラルネットワークにおける重みとバイアスは複数あるはずです。
例えば、\(W_1\)の場合、以下になります。
\(W_2\)の場合は、以下になります。
\(W_3\)の場合、、、
上記を重み分すべて計算する必要があります。
ニューラルネットワークの重みは何万・何十万個存在するので、なかなかしんどいです。
さらに、これらの重みが、例えば入力層→中間層の第１層の重みだと仮定します。
これらの重みを更新した場合、これら以降の入力値が変化してしまいます。その変化を考慮して次の層の重み変化量を計算することは非常に困難です。
これらの問題をうまくクリアしながら計算する方法があります。
「誤差逆伝播法」と呼ばれる方法です。
次回、誤差逆伝播法について解説していきます。
4. まとめ
今回はニューラルネットワークにおける学習について、また勾配法について解説しました。
次回も是非みてみてください！
5. 参考文献
斎藤康毅 著 「ゼロから作るDeep Learning ーPythonで学ぶディープラーニングの理論と実装」
Link
Search